uv16472
QUESTION : Montrez par les tableaux sémantiques ou le calcul des séquents qu'à partir des prémisses
'E' x : p(x , b) -> 'A' x : q(x) et 'A' x : p(a , x) on démontre
'A' x : (r(x , c) -> q(x))

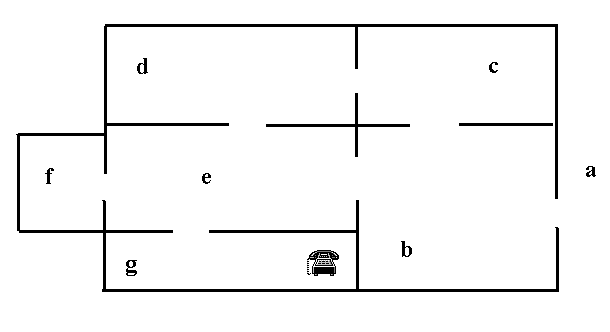
le téléphone est dans la pièce g. En Prolog : telephone(g).
les portes sont spécifiées par les faits Prolog (a symbolise l'extérieur):
porte(a,b). porte(b,e). porte(b,c). porte(d,e).
porte(c,d). porte(e,f). porte(g,e).
QUESTION 1 : construire le prédicat aller/3 qui retourne un chemin sans cycle pour aller d'une pièce à une autre ou de l'extérieur (a) à une pièce.
Appliquer votre prédicat pour atteindre le téléphone quand on vient de l'extérieur, c'est poser la question :
?- telephone(T) , aller(a,T , CHEMIN). ou bien
?- aller(a,T , CHEMIN) , telephone(T).
QUESTION 2 : Donnez l'ensemble des réponses à chacune de ces 2 questions et justifiez vos réponses
Dans les exercices sur le net on trouve cet exercice de tri simplifié : le drapeau hollandais. Enoncé informel : Les éléments d'un tableau de t(1..n) ne peuvent prendre qu'une des 3 valeurs : {rouge, bleu, blanc }. Le problème est de ranger ce tableau pour que tous les éléments bleus soient au début, suivis par les éléments blancs et fin de tous les éléments rouges du tableau initial.
JLD dit : J'AI FAIT LE BOULOT JUSQU'i et je me retrouve dans la situation suivante :
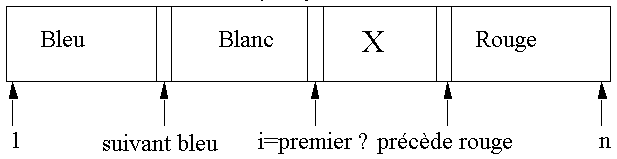
'A' x : ((x>=1 & x < sb) -> t(x) = bleu) & 'A' x : ((x>=sb & x =< pr) -> t(x)= blanc)& 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & 1 =< sb & sb < pr & pr =< n |
Informellement : on balaye le tableau de gauche à droite. On examine alors le premier élément NON encore traité et on le place avec ceux de sa couleur.
Plus précisément : s'il est blanc il est à sa place, on passe à l'examen de l'élément suivant. Si il est bleu on l'échange avec l'élément qui suit dernier élément bleu. Si il est rouge on l'échange avec l'élément qui précède le premier élément rouge. Dans ces 2 derniers cas on regarde ce qui a été rapporté pour remplacer l'élément en cours car si c'est un élément blanc on peut passer à l'examen de l'élément suivant.
{ 'A' x : ((x>=1 & x =< n) -> ((t(x) = bleu) v (t(x) = blanc) v (t(x) = rouge)) )} ;'
sb := 1 ; pr := n ; i := 1 ;
while i < pr
invariant { 'A' x : ((x>=1 & x < sb) -> t(x) = bleu) &
'A' x : ((x>=sb & x < i) -> t(x) = blanc) &
'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr & pr=<n }
variant {pr - i}
do
if t(i) = bleu
then ( t := t(i) ; t(i) := t(sb) ; t(sb) := t ; sb := sb+1
else
if t(i) = rouge
then t := t(i) ; t(i) := t(pr) ; t(pr) := t ; pr := pr-1 ;
end
end ;
if t(i) = blanc v sb > i then i := i+1 end )
end ;
%post-assertion :
{ 'A' x : ((x>=1 & x < sb) -> t(x) = bleu) & 'A' x : ((x>=sb & x =< pr) -> t(x) = blanc) &
'A' x : ((x>pr & x =< n) -> t(x) = rouge) & 0 =< sb & sb < pr & pr =< n }
|
On simplifie encore le problème : on ne dispose plus que de 2 couleurs (bleu et rouge).
Le tableau final ou " drapeau de PARIS " contient d'abord tous les éléments bleus suivis de tous les éléments rouges du tableau initial.
QUESTION : simplifiez l'exemple précédent (pré/post-condition , invariant , variant , programme) pour obtenir une solution du " drapeau de PARIS " et montrez la correction totale de votre programme.
On demande de réaliser une classe répertoire qui gère les couples nom/numéro de téléphone (On pensera pour la structure de données, en particulier, aux classes de l'api Collection).
QUESTION 1: Donner la spécification de cette classe sous forme d'une classe abstraite contenant les signatures de toutes les méthodes qui vous paraissent utiles à un tel répertoire. On spécifiera chacune de ces méthodes sous forme de pré et post assertion en langage courant ou pseudo-formel. On formulera éventuellement un invariant de classe.
QUESTION 2 : Implémenter cette classe abstraite en spécifiant les éventuels invariants de boucles en langage courant ou pseudo-formel.
QUESTION 3 : modifier cette classe pour que ses objets deviennent " cloneable " en profondeur.