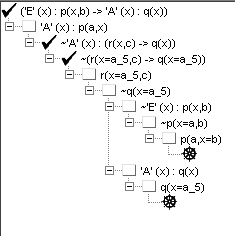
/* une diée de ce qui était attendu à la 2ème session 2003 ...

1- Preuves :

2- Prolog :

porte(a,b).
porte(b,e).
porte(b,c).
porte(d,e).
porte(c,d).
porte(e,f).
porte(g,e).

telephone(g).
aller(X,Y , T) :- aller(X,Y , [] , T).
aller(X,X , T,[X|T]).  % attention le chemin est " à l'envers "
aller(X,Y , L,T) :- 
	porte(X,Z) , not member(Z , L) , not member(Y,L) , 
	aller(Z,Y , [X|L] , T).
aller(X,Y , L,T) :- 
	porte(Z,X) , not member(Z , L) , not member(Y,L) , 
	aller(Z,Y , [X|L] , T).

?- aller(a , X , CHE) , telephone(X). %pas de réponse et négation NON sure
?- telephone(X) , aller(a , X , CHE).
	X = g   CHE = [g, e, b, a] ;
	X = g   CHE = [g, e, d, c, b, a] ;
	No

3-HOARE :

{ 'A' x : ((x>=1 & x =< n) -> (t(x) = bleu v t(x) = rouge) )} ; pr := n ; i := 1 ; while i =< pr invariant { 'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n } variant {pr - i+1} do if t(i) = bleu then i:= i+1 else /* t(i) = rouge */ t := t(i) ; t(i) := t(pr) ; t(pr) := t ; pr := pr-1 ; end end ; %post-assertion : { 'A' x : ((x>=1 & x =< pr) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & 0 =< pr & pr =<n}

A prouver : {P}; while B do S end ; {Q} P= 'A' x : ((x>=1 & x =< n) -> (t(x) = bleu v t(x) = rouge) ) & i=1 & pr=n Q= 'A' x : ((x>=1 & x =< pr) -> t(x) = bleu) &       'A' x : ((x>pr & x =< n) -> t(x) = rouge) &       0 =< pr &       pr =<n I ='A' x : ((x>=1 & x < i) -> t(x) = bleu) &     'A' x : ((x>pr & x =< n) -> t(x) = rouge) &     i=<pr+1 &     pr=<n B = i =< pr V = pr-i+1

(i)- P -> I : vrai par défaut (il n'existe pas x : x>=1 & x < 1 ni x : x>n & x =< n)

(ii)- {I & B} ; S ; {I} S instruction " if " donc 2 vérifications (a) t(i)=bleu {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n & i<pr} -> trivial car t(i)=bleu {'A' x : ((x>=1 & x < i+1) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n} i :=i+1 ; {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<p+1 & pr=<n} (aa) t(i)=rouge {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n & i=<pr} -> trivial {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x> pr & x =< n) -> t(x) = rouge) & i=< pr & pr-1 =<n & t(i)=rouge} t := t(i) ; t(i) n'a pas de propriété particulière dans la formule donc rien de nouveau: {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x> pr & x =< n) -> t(x) = rouge) & i=< pr & pr-1 =<n & t=rouge} t(i) := t(pr) ; {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x> pr & x =< n) -> t(x) = rouge) & i=< pr & pr-1 =<n & t=rouge} t(pr) := t ; montrer la propriété de t(pr) : {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x> pr & x =< n) -> t(x) = rouge) & i=< pr & pr-1 =<n & t(pr)=rouge} {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x> pr-1 & x =< n) -> t(x) = rouge) & i=< (pr-1)+1 & pr-1 =<n} pr := pr-1 ; {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n}

(iii) I & ~B -> Q {'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n & i>pr} (-> i=pr+1) -> donc i>pr et t(i) = rouge !!! 'A' x : ((x>=1 & x =< pr) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & 0 =< pr & pr =<n

(iv) : 'A' x : ((x>=1 & x < i) -> t(x) = bleu) & 'A' x : ((x>pr & x =< n) -> t(x) = rouge) & i=<pr+1 & pr=<n & i=<pr -> pr-i +1> 0 trivial

(v) en fait : V1 := pr-i ; if t(i)=bleu then i := i+1 else pr:= pr-1end ; {pr-i<V1} (a) cas t(i)=bleu {pr-i<pr-i+1} // toujours vraie V1 := pr-i +1 {pr-(i+1)+1<V1} i := i+1 {pr-i<V1} (b) cas t(i)=rouge { pr-i)<pr-i+1} // toujours vraie V1 := pr-i +1 {pr-1 -i+1<V1} pr := pr-1 {pr-i+1<V1}