ED n·4 Algorithmique et Programmation--------Corrigé

Exercice 1 : Compaction d'un tableau
 

Un tableau d'entiers contient de nombreuses occurrences de 0 et quelques valeurs non nulles. On désire modifier le tableau de telle sorte que tous les éléments nuls soient regroupés au début du tableau.
 

Question 1

Construire l'algorithme en suivant la méthode décrite ci-dessus.

 Solution

La méthode se décompose en quatre étapes:

Première étape : déterminer une hypothèse de récurrence.

Elle formalise l'idée choisie pour construire la solution du problème donné.

Soit T(1..n) le tableau à compacter

Pour déterminer une hypothèse de récurrence, on va considérer que le traitement est déjà engagé et que, par conséquent, un certain nombre d'éléments du tableau sont traités.
La situation courante peut être décrite ainsi : le tableau T(1..n) est vu comme la concaténation des trois tranches de tableau :

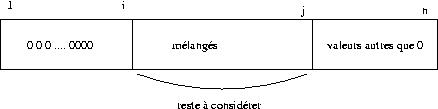
Cela constitue notre hypothèse de récurrence
 

Seconde étape : établir la condition d'arrêt de l'itération (CAI)

Pour que la solution soit atteinte, il faut que le tableau T(1..n) résulte de la concaténation des deux tranches :

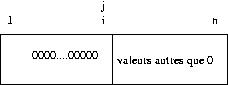
Autrement dit, il faut que le sous-tableau T(i+1..j) soit vide, c'est à dire qu'il ne possède aucun élément
ou encore que :

La condition d'arrêt de l'itération est donc :
j=i

Troisième étape : construire le corps de boucle

On suppose l'hypothèse de  récurrence  vérifiée  à une étape quelconque du traitement et on démontre qu'elle est encore vérifiée à l'étape suivante.
On procède  ainsi:

  1. se rapprocher de la solution
On va placer un élément qui se trouve dans le sous-tableau T(i+1..j) qui contient des valeurs non traitées.
On choisit, par exemple de parcourir ce sous-tableau de gauche à droite. Dans ce cas, on place l'élément T(i+1).
On aurait pu tout aussi bien placer T(j) si l'on considère un parcours inverse.

Choisissons la seconde solution, l'algorithme pour placer T(j) est :

si T(j)=0
alors
    permuter T(j) et T(i+1)
sinon
    ne rien faire
finsi

On a bien ajouter T(j) à la zone à laquelle il appartient, mais l'hypothèse de récurrence n'est plus vérifiée. En effet T(j) ne contient pas une valeur quelconque comme le stipule l'hypothèse de récurrence mais la valeur 0.
 

  1. retrouver l'hypothèse de récurrence.
La situation actuelle est la suivante :

Ou bien si la première solution avait été choisie

Pour revenir à l'hypothèse de récurrence, on complète l'algorithme précédent :

si T(j)=0
alors
    permuter T(j) et T(i+1);
    i:=i+1;
sinon
    ne rien faire;
    j:=j-1;
finsi

Quatrième étape : initialisation des variables

Le raisonnement se termine par la preuve que l'hypothèse de récurrence est vérifiée avant que le traitement ne soit commencé. Cette quatrième étape correspond à l'initialisation.

En cas de succès du raisonnement, l'hypothèse de récurrence devient l'invariant de l'algorithme. Cet invariant se transforme en un commentaire informatif du programme. Les preuves de correction d'un programme sont facilitées par sa présence.

Seules deux variables sont utilisées : i et j. Elle doivent vérifier l'hypothèse avant le début du traitement.
La situation initiale est représentée par le tableau :

On constate que si l'on compare cette situation à celle de l'hypothèse, elles ne peuvent coincider que si les sous-tableaux T(1..i) et T(j+1..n) sont vides.
Les équations i-1+1=0 et n-(j+1)+1=0 doivent être résolues.
D'où

i=0
j=n





Algorithme complet

début
    i<-0;
    j<-n;
-- T(1..i) contient uniquement des valeurs nulles
-- T(i+1..j) contient des valeurs quelconques
-- T(j+1..n) ne contient que des valeurs différentes de 0
    tant que i<j faire
         si T(j)=0
        alors
                  permuter T(j) et T(i+1);
                   i<-i+1;
        sinon
                    ne rien faire;
                    j<-j-1;
        finsi;
    fin tant que;
fin.
 

Exercice d'application

Suivre la même démarche avec une autre hypothèse de récurrence.