


Next: Types et objets en
Up: Polymorphisme dans les langages
Previous: Le polymorphisme paramétrique
Le polymorphisme d'inclusion est plus couramment connu sous le nom de
sous-typage. Dans ce genre de polymorphisme on ne
parle pas d'instances de types, mais d'inclusion entre types.
Définition (Sous-type):
Un type t' est un sous-type (ou est inclus dans) un type
t si n'importe quelle opération définie sur t
est aussi définie sur les éléments du type t'. On dit qu'un
objet de type t' peut remplacer sans danger un
objet de type t, ou encore
qu'un objet de type t' peut être vu comme ayant le type t.
Nous noterons
 la relation ``le type t'
est un sous-type du type t''.
la relation ``le type t'
est un sous-type du type t''.
Exemple 1:
On peut voir
le type des entiers comme un sous-type du
type des réels3: tout entier peut être vu
aussi comme un réel, et l'ensemble
de tous les entiers est inclus dans l'ensemble de tous les réels.
Exemple 2:
Le type colorpoint est un sous-type du type point.
En effet, toute opération définie sur les points est
aussi définie sur les points avec couleur, et donc, un objet
de type colorpoint peut être utilisé sans danger
là où un point est attendu. La notation
p:> point est lue ``p vu comme un point''.
Ainsi, la fonction
# let origin (p) = (p :> point)#getx = 0;;
val origin : < getx : int; move : int -> unit; .. > -> bool = <fun>
peut-être appliquée sur des objets de type colorpoint.
Le sous-typage est intéressant car il permet l'usage
polymorphe des valeurs: une même valeur (ou fonction) peut avoir
plusieurs types, et en particulier tous ses super-types.
Par exemple, la constante 3 a le type entier mais aussi
le type réel car le type entier est un sous-type de
du type réel. Un point coloré a le type colorpoint mais
a aussi le type point.
Définition:(Polymorphisme d'inclusion ou
sous-typage)
Si a a le type 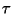 ,
et si
,
et si 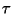 est un sous-type
de
est un sous-type
de 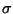 ,
alors a a aussi le type
,
alors a a aussi le type 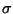 .
Une autre formulation est: si
a a le type
.
Une autre formulation est: si
a a le type 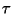 ,
et si
,
et si 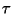 est un sous-type
de
est un sous-type
de 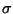 ,
alors a peut être vu comme de type
,
alors a peut être vu comme de type 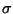 .
.
Cetee notion est étudié plus en détail un peu plus tard dans ces notes.



Next: Types et objets en
Up: Polymorphisme dans les langages
Previous: Le polymorphisme paramétrique
Maria-Viginia Aponte
2001-04-10