


Next: Relation entre héritage et
Up: Sous-typage
Previous: Les méthodes binaires
Soient b et a deux classes telles que
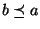 .
La règle de typage entre objets impose
que les types des méthodes de b soient des sous-types de celles
dans a. Lorsque leurs types sont atomiques
(par exemple compte, compteremunere, etc.), il est
facile de les comparer par sous-typage: si
f dans b est de type
compteremunere et dans a elle
a le type compte, nous pouvons facilement chercher à établir
.
La règle de typage entre objets impose
que les types des méthodes de b soient des sous-types de celles
dans a. Lorsque leurs types sont atomiques
(par exemple compte, compteremunere, etc.), il est
facile de les comparer par sous-typage: si
f dans b est de type
compteremunere et dans a elle
a le type compte, nous pouvons facilement chercher à établir
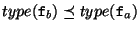 (où
(où
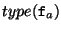 désigne le type de f dans
la classe a), c.a.d.,
désigne le type de f dans
la classe a), c.a.d.,
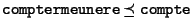 .
.
En revanche, que se passe-t-il si les méthodes à comparer
sont des fonctions?
Comment savoir si deux types de fonctions sont en relation de sous-typage?
Posons le cas suivant:
class a =
...
method f: t -> q
...
end
class b =
...
method f: m -> n
end
Pour établir
 il faut
vérifier
il faut
vérifier
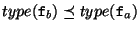 ,
c.a.d.,
,
c.a.d.,
 .
Quand est-ce que ces deux
types fonctionnels sont en relation de sous-typage?
.
Quand est-ce que ces deux
types fonctionnels sont en relation de sous-typage?
Règle (Sous-typage entre fonctions):
Deux types fonctionnels,
(
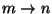 )
et (
)
et (
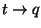 )
sont en relation de sous-typage:
)
sont en relation de sous-typage:
ssi
-
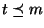 et
et
-
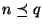 .
.
Justifions cette règle. Nous supposons que les types fonctionnels
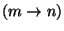 et
et
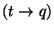 sont les types
de la méthode f des classes b et a plus haut. Pour distinguer
les deux méthodes nous les appelons fa et fb:
sont les types
de la méthode f des classes b et a plus haut. Pour distinguer
les deux méthodes nous les appelons fa et fb:
Nous faisons également les hypothèses suivantes:
-
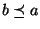 ,
,
- il existe une fonction autre qui prend un argument
r : q (voir sa définition plus bas),
- il existe une fonction h (voir définition plus bas)
qui envoie
le message f à un objet o de type a. Lors
de cet envoi, elle fournit un argument x:t à f,
alors que cette méthode dans a attend prcisement
un argument de type t.
let autre (r: q) = ....
let h(o: a, x: t) = autre(o#f(x));;
D'après ces hypothèses et définitions nous constatons:
- le code o#f(x) est bien typé. En effet, puisque
o:a, cet objet possède bien une méthode f, dont
l'argument attendu est de type t. Le type
déclaré pour x est précisement t,
- le code autre(o#f(x)) est aussi bien typé,
car le type résultat de f dans a
est q, et que celui-ci est le type attendu pour l'argument de
autre.
- ces hypothèses ne retirent
rien à la généralité de notre exemple.
Justifions maintenant la règle de typage:
- 1.
- (Justification de
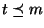 ):
Par hypotèse
):
Par hypotèse
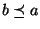 ,
on peut appliquer la fonction h
à un objet (ob : b). L'appel se transforme en
,
on peut appliquer la fonction h
à un objet (ob : b). L'appel se transforme en
dans cet appel, quel est le type de
x? Il est déclaré de même type (t) que les arguments de fa, mais
il doit pouvoir être vu
comme ayant le type de l'argument de fb ( c.a.d., comme ayant
le type m), donc
Notons que la
relation inverse
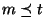 est impossible:
fb ne pourrait pas recevoir un argument
de type t. Un appel
est impossible:
fb ne pourrait pas recevoir un argument
de type t. Un appel
serait alors incorrecte.
- 2.
- (Justification de
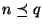 ): la fonction
autre attend un argument de même type ou plus petit que
celui résultat d'un appel à fa. Mais, son argument
peut-être du type du résultat de fb, donc:
): la fonction
autre attend un argument de même type ou plus petit que
celui résultat d'un appel à fa. Mais, son argument
peut-être du type du résultat de fb, donc:
ainsi, les deux appels autre(p) et autre(w) sont correctes,
pour p:n et w:q.
On dit que la règle de sous-typage entre fonctions et
co-variante pour les types résultat (le type
résultat du plus petit des deux types est plus
petit (va dans le même sens)
que le type résultat du plus grand des deux),
alors qu'elle est contre-variante pour les types
argument (elle change de sens).



Next: Relation entre héritage et
Up: Sous-typage
Previous: Les méthodes binaires
Maria-Viginia Aponte
2001-04-10
![]() .
La règle de typage entre objets impose
que les types des méthodes de b soient des sous-types de celles
dans a. Lorsque leurs types sont atomiques
(par exemple compte, compteremunere, etc.), il est
facile de les comparer par sous-typage: si
f dans b est de type
compteremunere et dans a elle
a le type compte, nous pouvons facilement chercher à établir
.
La règle de typage entre objets impose
que les types des méthodes de b soient des sous-types de celles
dans a. Lorsque leurs types sont atomiques
(par exemple compte, compteremunere, etc.), il est
facile de les comparer par sous-typage: si
f dans b est de type
compteremunere et dans a elle
a le type compte, nous pouvons facilement chercher à établir
![]() (où
(où
![]() désigne le type de f dans
la classe a), c.a.d.,
désigne le type de f dans
la classe a), c.a.d.,
![]() .
.
![]() )
et (
)
et (
![]() )
sont en relation de sous-typage:
)
sont en relation de sous-typage:
![]() et
et
![]() sont les types
de la méthode f des classes b et a plus haut. Pour distinguer
les deux méthodes nous les appelons fa et fb:
sont les types
de la méthode f des classes b et a plus haut. Pour distinguer
les deux méthodes nous les appelons fa et fb: