une idée de ce qui était attendu ...

1-Preuve :

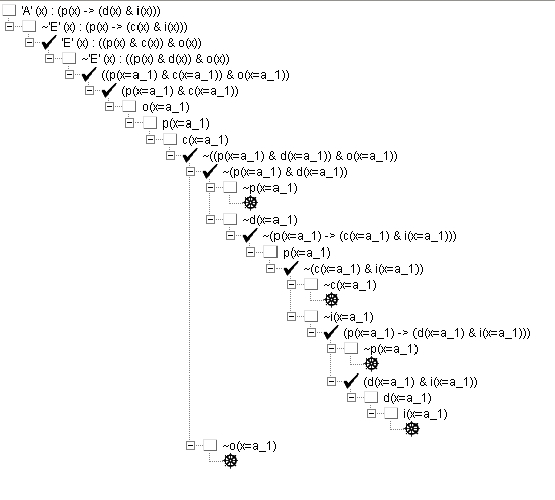
x est un développeur : P(x) ,
x est doué : D(x) ,
x est intelligent : I(x) ,
x développe en C : C(x) ,
x développe en Java : O(x).
Alors : (cf. formes aristotéliciennes)
Les développeurs sont doués ou intelligents : x (P(x) -> (D(x) v I(x)) ;
les développeurs intelligents ne développent pas en C : ¬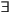x (P(x) -> (I(x) & C(x)) ;
il y a des développeurs qui développent en C et en Java : 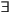x (P(x) & (C(x) & O(x)) ;
Conclusion : il y a des développeurs doués qui développent en Java : 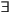x (P(x) & (D(x) & O(x))

transposé(TVIDE , []) :- tabVide(TVIDE).
transposé(TAB , [LIGNE |TRANS]) :-
	construire1ligne(TAB , TA , LIGNE) ,
	transposé(TA , TRANS).

tabVide([]).
tabVide([[]|TV]) :- tabVide(TV).

construire1ligne([] , [] , []).
construire1ligne([[EL|LI]|TAB] , [LI|TA] , [EL|LGN]) :-
	construire1ligne(TAB , TA , LGN).

(1)Invariant :{INV} = {R=(I-1)*N+J & ii,j,r (((1=<i=<I-1 & 1=<j=<N) v (i=I & 1=<j=<J)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j) = Vect(r)};
PréAsserttion P = (I=1 & J=0 & R=0 & NbrElem=M==*N)
il faut montrer que P -> INV : on a bien R=(I-1)*N+J , le reste est vrai par défaut car 1=<j=<0 & 1=<r=<0 n'existent pas.

(2)INV est l'invariant de la boucle. En remontant et 2 vérifications pour l'instruction 'ifThenElse': 
(2-1)
(INV & R<NbreElem)  -> Rem4 ?  : trivial

{Rem4}={J<N & R+1=(I-1)*N +J+1 & i,j,r (((1=<i=<I-1 & 1=<j=<N) v (i=I & 1=<j=<J+1)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R+1)=Tab(I,J+1)};

{Rem3}={J<N & R+1=(I-1)*N +J+1 & i,j,r (((1=<i=<I-1 & 1=<j=<N) v (i=I & 1=<j=<J+1)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R+1)=Tab(I , J+1)};

R := R+1 ;

{Rem2}={J<N & R=(I-1)*N+J+1 & i,j,r (((1=<i=<I-1 & 1=<j=<N) v (i=I & 1=<j=<J+1)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R)=Tab(I,J+1)};

J := J+1 ;

{Rem1}={INV & Vect(R)=Tab(I,J)};

Vect(R) := Tab(I,J);

{INV};

(2-2)
(INV & R<NbreElem)  -> Rem5 ?  : trivial
{Rem5}={J=N & R+1=(I-1)*N+N+1 & i,j,r (((1=<i=<I & 1=<j=<N) v (i=I+1 & 1=<j=<1)) & 1=<r=<R+1) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R+1)=Tab(I+1,1)};
{Rem4}={J=N & R+1=(I)*N +1 & i,j,r (((1=<i=<I & 1=<j=<N) v (i=I+1 & 1=<j=<1)) & 1=<r=<R+1) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R+1)=Tab(I+1 , 1)};
R := R+1 ;
{Rem3}={J=N & R=(I)*N +1 & i,j,r (((1=<i=<I & 1=<j=<N) v (i=I+1 & 1=<j=<1)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R)=Tab(I+1,1)};
I := I+1 ;
{Rem2}={R=(I-1)*N +1 & i,j,r (((1=<i=<I-1 & 1=<j=<N) v (i=I & 1=<j=<1)) & 1=<r=<R) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & Vect(R)=Tab(I,1)};
J := 1 ;
{Rem1}={INV & Vect(R)=Tab(I,J)};
Vect(R) := Tab(I,J);
{INV};
(3) montrer que (INV & R=NbreElem)  ->   la post-Assertion : 
{ i,j,r (1 =< i =< M & 1=< j =< N & 1 =< r =< M*N) -> r = (i-1)*N+j & Tab(i,j) = Vect(r) }
R=NbreElem=M*N assure que I=M et J=N donc (INV & R=NbreElem) s'écrit : 
(i,j,r (((1=<i=<M-1 & 1=<j=<N) v (i=M & 1=<j=<N)) & 1=<r=<M*N) -> r=(i-1)*N+j & Tab(i,j)=Vect(r) & R=M*N) et ((1=<i=<M-1 & 1=<j=<N) v (i=M & 1=<j=<N)) est identique à (1 =< i =< M & 1=< j =< N)
Alors (INV & R=NbreElem) et la postAssertion sont identiques. QED

class EnsembleOrdonne extends Ensemble implements SortedSet{
  protected Comparator       comp;
  public static final Comparator CROISSANT = new Comparator(){
    public int compare(Object o1, Object o2){
      if (o1 instanceof Comparable && o2 instanceof Comparable)
	return ((Comparable)o1).compareTo(o2);
      else
	throw new ClassCastException();
    }
  };
  public static final Comparator DECROISSANT = new Comparator(){
    public int compare(Object o1, Object o2){
      if (o1 instanceof Comparable && o2 instanceof Comparable)
	return -((Comparable)o1).compareTo(o2);
      else
	throw new ClassCastException();
    }
  };
  public EnsembleOrdonne(Comparator comp){
    super();
    this.comp = comp;
  }

  public SortedSet subSet(Object fromElement, Object toElement){
    EnsembleOrdonne s = new EnsembleOrdonne(this.comp);
    if( contains(fromElement) && contains(toElement)){
      Iterator it = this.iterator();
      Object obj = it.next();
      while (((Comparable)obj).compareTo(fromElement)!=0){ obj = it.next();}
      s.add(fromElement);
      while (((Comparable)obj).compareTo(toElement)!=0){
	s.add(obj);
	obj = it.next();
      }
      s.add(toElement);
    }
    return s;
  }
  public SortedSet headSet(Object toElement){ 
    SortedSet s = new EnsembleOrdonne(this.comp);
    if( contains(toElement)){
      Iterator it = this.iterator();
      Object obj = it.next();
      while(it.hasNext() && ((Comparable)obj).compareTo(toElement)!=0){ 
	s.add(obj);
	obj = it.next();
      }
    }
    return s;
  }
  public SortedSet tailSet(Object fromElement){
    SortedSet s = new EnsembleOrdonne(this.comp);
    s = this.subSet(fromElement,last());
    s.remove(fromElement);
    return s;
  }
  public Object first(){ return table.firstElement();}
  public Object last(){ return table.lastElement();}
  public boolean add(Object o){
      if (isEmpty()) {
	super.add(o);
      }else if (!this.contains(o)){
	      int i = 0;
	      while (i < size() && (comp.compare(o,table.elementAt(i)) > 0)){
		i++;
	      }
	      table.insertElementAt(o , i);
      }
     return true;
  }
  public Comparator comparator(){return comp;}
}

/* *** fin *** */