énoncé deuxième session 2004

uv16472

A la première session on proposait l'ensemble de 4 formules logiques :

(i) (x , y)(aGauche(x , y) -> plusGrand(x , y))

(ii) (x)(cube(x) -> petit(x ))

(iii) (x)(tétraèdre(x) -> petit(x ))

(iv) (x , y)(( petit(x) & petit(y))-> ~plusGrand(x , y))

On ne sait pas représenter cet ensemble de formules par un programme Prolog à cause de (iv) qui donnerait une tête de clause avec une négation. Alors on contourne le problème en remplaçant ~plusGrand(x , y) par un nouveau prédicat memeTaille :

(x , y)(( petit(x) & petit(y))-> memeTaille (x , y))

(x , y)(( ~plusGrand(x , y) & ~plusGrand(y , x))-> memeTaille(x , y))

D'autre part, on possède 2 cubes : c1 et c2 et un tétraèdre tt . Cela se représente en Prolog par 3 faits :

cube(c1).

cube(c2).

tétraèdre(tt).

QUESTION 1

Donnez le programme Prolog constitué des faits ci-dessus et des clauses correspondant à l'ensemble modifié des formules

Pour calculer la sémantique de point fixe d'un programme avec négation il faut stratifier le programme.

QUESTION 2	Donnez le graphe de dépendances du programme et les strates permettant de calculer la sémantique
QUESTION 3	Donnez la sémantique de point fixe du programme.
QUESTION 4	Donnez la formule du complété du programme.

étudiant(<NOM> , <MATRICULE> , <LISTE de NOTES>).

Exemple :

étudiant(et1 , i12345 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et2 , i12346 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

On veut associer à chaque étudiant la liste de ses notes pour les 15 devoirs de l'année (0 si le devoir n'a pas été rendu). Exemple :

A étudiant(et1,i12345 , [dh(1,5) , dh(2,3) , dh(4,2) , dh(8,5) , dh(3,0) ])

correspondra élève(et1 , i12345 , [5,3,0,2,0,0,0,5,0,0,0,0,0,0,0])

ou bien élève(et1 , i12345 , [0,0,0,0,0,0,0,5,0,0,0,2,0,3,5])

On a écrit :

eln(étudiant(E , M , LDH) , élève(E , M , LN)) :- ldh2ln(LDH , LN).

ldh2ln(LDH , LN) :- ldh2ln(15 , LDH , LN). % 15 : 15 devoirs dans l'année

ldh2ln(0 , _ , []).

ldh2ln(N , LDH ,[0|LN]) :- /* à compléter */

ldh2ln(N , LDH ,[Note|LN]) :- % Note : note obtenue au devoir n° N
                                /* à compléter */

QUESTION 1	compléter le Prédicat ldh2ln/3 qui permet d'obtenir la liste des notes aux devoirs d'un élève.
QUESTION 2	La liste obtenue est-elle ordonnée du DH15 au DH1 ou bien du DH1 au DH15 ?

Les Automates finis ou AF sont des reconnaisseurs, i.e. ils permettent de décider si des chaînes de symboles (pris dans un alphabet donné) correspondent, "respectent" un certain modèle. Dans le cas des AF les chaînes reconnues sont appelées " expressions régulières ".

On représente les AF sous la forme d'un 5-uplet

<'Etats' , 'Symboles' , 'Transition ', 'EtatInitial ', 'EtatsFinals'>

· 'Etats' : un ensemble fini d'états (que peut prendre l'AF)

· 'Symboles' : un ensemble fini de symboles 'reconnus' par l'AF (ou alphabet de l'AF)

· 'EtatInitial' : un état particulier de 'Etats' dit état de départ.

· 'EtatsFinals' : un sous ensemble de 'Etats' des états dits finals

· Transition : une fonction t : 'Etats' x 'Symboles' ---> 'Etats' qui décrit les changements d'état de l'AF en fonction du Symbole en entrée.

Un AF est dit NON-déterministe si il existe plusieurs transitions différentes à partir d'un état donné pour un même symbole.

On représente souvent aussi les AF par "des ronds et des flèches" : L'automate fini représenté sur le dessin ci dessous est une version NON-déterministe de l'AF vu dans le DH17. Les chaînes reconnues par cet AF sont " toutes les chaînes de {a , b} qui se terminent par abb "

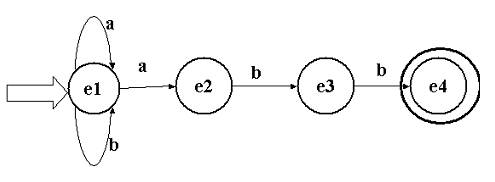
en Prolog la représentation des AF et de la reconnaissance est immédiate. L'expression à reconnaître est représentée dans une liste de symboles. Par exemple pour l'AF ci dessus :

départ(e1).

final(e4).

transition(e1,a , e1).

transition(e1,a , e2).

transition(e1,b , e1).

transition(e2,b , e3).

transition(e3,b , e4).

reconnaissance(EXPLISTE) :- départ(E), reconnaissance(EXPLISTE , E).

reconnaissance([A|EXPLISTE] , E) :- transition(E,A , ES) ,

reconnaissance(EXPLISTE , ES).

reconnaissance([] , E) :- final(E).

?- reconnaissance([a,a,a,a,a,a,b,a,b,b]).

Yes

?- reconnaissance([a,a,a,a,a,a,b,a,b]).

No

La reconnaissance des Expressions régulières s'exprime aussi simplement par une DCG, par exemple pour l'AF ci dessus :

e1 --> [a] , e1.

e1 --> [a] , e2. % NON-déterminisme

e1 --> [b] , e1.

e2 --> [b] , e3.

e3 --> [b] , e4.

e4 --> []. %pour voir e4 dans la grammaire

?- e1([a,a,a,a,a,a,b,a,b,b] , []).

yes

?- e1([a,a,a,a,a,a,b,a,b,a,b] , []).

No

?-

QUESTION1	Donnez le dessin de l'AF et le programme Prolog de l'AF et la DCG de l'AF qui reconnaît " toutes les chaînes de {a , b} qui se terminent par bab "
QUESTION2	Réunir les deux dessins des deux AF , les deux programmes Prolog des deux AF et les deux DCG des deux AF pour obtenir un AF qui reconnaît et les chaînes du premier AF et les chaînes de la question 1.
QUESTION3	Transformer le programme Prolog de l'AF de l'exemple et augmenter sa DCG pour que chaque reconnaissance retourne le type de la chaîne reconnue : ABB ou BAB

Remarque : il est possible de répondre à ces trois questions en une seule fois (i.e. réponse à la question 3 bien commentée…).

4-Java (5 points) :  Pattern Observer

On vous demande d'implémenter en Java un exemple du " pattern " observateur.

Rappelons que ce "pattern" permet à un objet (Observer) d'observer un autre objet (Subject). Pour cela le sujet (Subject) autorise les observateurs (Observer) à s'inscrire auprès de lui. Le sujet (Subject) gère la liste des observateurs inscrits et lors d'une modification de son état interne notifie tous les observateurs inscrits du fait qu'une mise à jour (update) a eu lieu.

Observateurs et sujets implémentent l'interface correspondante parmi les deux suivantes :

public interface Subject {
    public void addObserver( Observer o );
    public void removeObserver( Observer o );
}

public interface Observer {
    public void update( Subject o );
}

QUESTION1

On vous demande tout d'abord d'implémenter une classe qui sera sujet de l'observation dont la fonction est simplement de conserver une collection d'entiers.

Pour cela complétez le code de la classe suivante :

import java.util.*;

abstract public class IntegerDataBag implements Subject {
    private List intergerBAG = new ArrayList();
    private List observers = new ArrayList();

// ajouter un entier à la collection
public void add( Integer i ) { /* à compléter…*/}

// supprimer un entier de la collection
public Integer remove( int index ) { /* à compléter…*/}

//retourne un itérateur sur la collection intergerBAG
public Iterator iterator() { /* à compléter…*/}

//alerte les observateurs d'une modification de la collection
private void notifyObservers() { /* à compléter…*/}

}

QUESTION2

On demande maintenant d'implémenter (en complétant les classes ci dessous ) 2 observateurs de cette liste d'entier.

Le premier IntegerAdder observe toute modification d'un ensemble et une fois prévenu imprime la nouvelle somme des valeurs de celui-ci.

Le deuxième IntegerPrinter imprime la liste à chaque nouvelle modification qui lui est notifiée.

import java.util.Iterator;

public class IntegerAdder implements Observer {

private IntegerDataBag bag;

public IntegerAdder( IntegerDataBag bag ) {
    this.bag = bag;
    bag.addObserver( this );
}

public void update( Subject o ) { /* à compléter */ }

}

import java.util.Iterator;

public class IntegerPrinter implements Observer {

private IntegerDataBag bag;

public IntegerPrinter( IntegerDataBag bag ) {
   this.bag = bag;
    bag.addObserver( this );

}

public void update( Subject o ) { /* à compléter */ }

}

Ci-dessous un programme de test de ces classes qui précisera le contexte d'usage des implémentations qui vous sont demandées.

public class Driver {

public static void main( String [] args ) {

Integer i1 = new Integer( 1 ); Integer i2 = new Integer( 2 );

Integer i3 = new Integer( 3 ); Integer i4 = new Integer( 4 );

Integer i5 = new Integer( 5 ); Integer i6 = new Integer( 6 );

Integer i7 = new Integer( 7 ); Integer i8 = new Integer( 8 );

Integer i9 = new Integer( 9 );

IntegerDataBag bag = new IntegerDataBag();

bag.add( i1 ); bag.add( i2 ); bag.add( i3 ); bag.add( i4 );

bag.add( i5 ); bag.add( i6 ); bag.add( i7 ); bag.add( i8 );

IntegerAdder adder = new IntegerAdder( bag );

IntegerPrinter printer = new IntegerPrinter( bag );

// adder and printer add themselves to the bag

System.out.println( "About to add another integer to the bag:" );

bag.add( i9 );

System.out.println("");

System.out.println("About to remove an integer from the bag:");

bag.remove( 0 );

}

}

QUESTION3

décrivez les entrées/sorties générées par vos observateurs compte tenu de ce 'main'.

Rappel de l'interface List :

public interface List extends Collection{ void add(int index, Object element) ; boolean add(Object o) ; boolean addAll(int index, Collection c) ; void clear() ; boolean containsAll(Collection c) ; boolean equals(Object o) ; Object get(int index) ; int hashCode() ; int indexOf(Object o) ; boolean isEmpty() ; Iterator iterator() ; int lastIndexOf(Object o) ; ListIterator listIterator() ; ListIterator listIterator(int index) ; Object remove(int index) ; boolean remove(Object o) ; boolean removeAll(Collection c) ; boolean retainAll(Collection c) ; Object set(int index, Object element) ; int size() ; List subList(int fromIndex, int toIndex) ; Object[] toArray() ; Object[] toArray(Object[] a) ; }