enoncé 2 --- 2002

énoncé deuxième session 2002

uv16472

On vous demande de prouver que "bob court plus vite que jeannot" est conséquence logique des 7 affirmations suivantes :

Les chevaux courent plus vite que les chiens.
les pointers courent plus vite que les lièvres.
les pointers sont des chiens.
si x court plus vite que y et si y court plus vite que z alors x court plus vite que z.
bob est un cheval
rex est un pointer
jeannot est un lièvre.

on a formalisé le problème pour le soumettre au DJProver :
['A' (x,y) : ((h(x) & d(y)) -> cpv(x,y) ),
 'A' (y,x) : ((p(y) & r(x)) -> cpv(y,x)),
 'A' y : (p(y) -> d(y)),
 'A' (x,y,z) : ((cpv(y ,z) & cpv(z,x)) -> cpv(y,x)),
  h(bob),
  p(rex),
  r(jeannot) 
 ] |- 
      cpv(bob , jeannot).
QUESTION 1.1 : Donnez la version Prolog de cette énigme en reprenant le formalisme ci dessus : quel programme ? quelle question ?
QUESTION 1.2 : Pourquoi ne peut-on pas atteindre la sémantique arrière de ce programme ?
QUESTION 1.3 : Si l'univers de Herbrand est réduit à {bob , rex , jeannot} , quelle est la base de Herbrand du programme.
QUESTION 1.4 : Donnez la sémantique en chaînage avant du programme.

2-Prolog/DATALOG VS SQL (4 points) :

Soit la table 'DH' d'une Base de Données :

DH
Matricule DH Note

I12345 5 1

I12345 6 2

I01234 4 3

I12345 7 3

I01234 6 3

I12345 8 2

I01234 8 1

I23456 5 1

I23456 4 2

I23456 3 3

I12345 2 3

DH
Matricule	DH	Note
I12345	5	1
I12345	6	2
I01234	4	3
I12345	7	3
I01234	6	3
I12345	8	2
I01234	8	1
I23456	5	1
I23456	4	2
I23456	3	3
I12345	2	3

La première ligne rappelle le nom des attributs.

QUESTION 2.1 : Donner la relation dh/3 équivalente à cette table en Prolog/DATALOG

2.2 : En Prolog on doit avoir recours à "assert/retract" pour programmer un compteur :

 
cpt(N) :- %incrémentation
     retract('CPT'(N)), ! ,  %récupération destructive de la valeur courante
     NN is N+1,              %incrémentation
     assert('CPT'(NN)).      %enregistrement de la nouvelle valeur
cpt(0) :- assert('CPT'(1)).  %initialisation

QUESTION 2.2 : Utiliser un tel compteur pour programmer en Prolog l'équivalent de la requête SQL

SELECT count(*) FROM DH

2.3: programmer en Prolog l'équivalent de la requête SQL

SELECT * FROM DH WHERE note=3

le programmeur doit se souvenir que le champs 'note' est le troisième argument de la relation dh.

Pour éviter cet inconvénient on ajoute à la relation dh/3 le fait table(dh('Matricule' , 'DH' , 'Note')).

et le prédicat prédéfini Prolog arg/3 permet d'utiliser un numéro d'argument à la place d'un nom d'attribut :

arg(?Arg, +Term, ?Value)
Term doit être instancié à un terme, Arg à un entier compris entre 1 et l'arité du terme.
Value est unifié au Arg-tième argument de Term.
Arg peut être non instancié et dans ce cas Value sera unifié avec les arguments successifs du terme (à partir de 1 ).
Si l'unification réussit, Arg est unifié avec le numéro de l'argument.
On atteint les autres solutions par Backtrack.
Le prédicat arg/3 échoue "silencieusement" si Arg= 0 ou Arg > arité de Term et léve l'exception domain_error(not_less_then_zero, Arg) si Arg <0.

QUESTION 2.3: Donner le programme Prolog général équivalent aux requêtes SQL de la forme :

SELECT * FROM DH WHERE <Champs>=<Valeur>

3-DCG + SEM (8 points) : Soient les nombres rationnels Q positifs ou nuls, représentés par des fractions (notées #) de nombres entiers :

N= A #B (B > 0) ou bien N = A si le dénominateur est 1 , A et B étant des entiers positifs ou nuls.

Soient les expressions arithmétiques sur les seuls opérateurs (+ , * , /) sur Q définies par la syntaxe abstraite :

1-Catégories syntaxiques :

e, e1, ... pour les Expressions

o, o1, ... {+ , * , /}

q, q1, ... pour les nombres Rationnels

n, n1, ... pour les Entiers Positifs ou nuls

2- Définitions

e ::= e1 o e2 | q

q ::= n | n1 #n2

L'évaluation d'une expression arithmétiques sur les rationnels retourne un nombre rationnel 'normalisé' i.e. soit un entier soit une fraction dont le numérateur et le dénominateur sont premiers entre eux (après évaluation on a encore divisé numérateur et dénominateur par le 'plus grand diviseur commun' des deux).
Programme Prolog du calcul du PGDC de 2 entiers Positifs

pgdc(A,A,A).

pgdc(A , B , PGDC) :- A>B , AA is A-B , pgdc(AA , B , PGDC).
pgdc(A , B , PGDC) :- A<B , BB is B-A , pgdc(A , BB , PGDC).

QUESTION 3.1 (Prolog) : Donnez le prédicat Prolog de normalisation des nombres rationnels : ?- normeQ(3#6, 1#2). Et aussi ?- normeQ(121#11, 11).

QUESTION 3.2(Sémantique Structurelle) : Donnez la version Prolog des règles d'inférence de l'évaluation de ces expressions et quelle est l'évaluation de

(456#101 + 33#2)*(18#47 + 24#7) / (1#181) ?

Rappels :

A#B + C#D =(A*D + C*B)#B*D
A#B *C#D =(A*C) #( B*D)
(A#B)/(C#D) = (A*D)# (B*C)

pgdc(A,A,A).
pgdc(A , B , PGDC) :- A>B , AA is A-B , pgdc(AA , B , PGDC).
pgdc(A , B , PGDC) :- A<B , BB is B-A , pgdc(A , BB , PGDC).

Une grammaire concrète de ces expressions est sous forme DCG :

exq --> tq , ['+'] , exq.
exq --> tq.
tp  --> fq , om , tq.
tq  --> fq.
fq  --> ['('] , exq , [')'].
fq  --> [X] , {integer(X)}.
fq  --> [X1] , ['#'] , [X2] , {integer(X1) , integer(X2)}.

om --> ['*'].
om --> ['/'].

QUESTION 3.3 (DCG) : Augmentez cette grammaire pour permettre l'évaluation d'une expression pendant son analyse.

4-Java (4 points) :



 Enoncé : On vous demande de programmer en Java une application simple du pattern " état transition "
dont voici les diagrammes UML  :
   

 

 

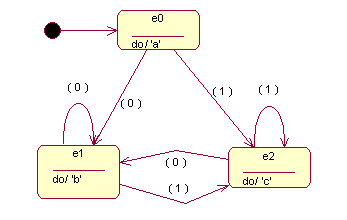
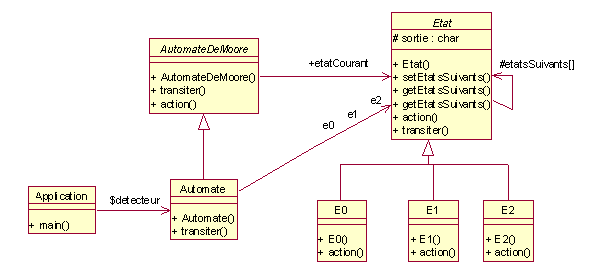Vous trouverez ci-dessous le texte du programme spécifier formellement au moyen d'ESC/Java :
Nous vous demandons de compléter le corps des méthodes avec toute la rigueur compatible avec la spécification associée..

abstract class AutomateDeMoore{
  public Etat etatCourant;
   //@ invariant etatCourant != null;

   public AutomateDeMoore(){  //@ assume etatCourant != null;}

   //@ requires entree>=0 & entree<etatCourant.etatsSuivants.length;
   //@ modifies etatCourant;
   //@ ensures \result==etatCourant;
   //@ ensures etatCourant==\old(etatCourant).etatsSuivants[entree];
   public Etat transiter(int entree){ …





   }
   
 
// la sortie est associée à l'état courant (Moore)
   //@ modifies etatCourant.sortie;
   //@ ensures \result==etatCourant.sortie;
   public char action(){


   }
}

class Automate extends AutomateDeMoore{

   Etat e0,e1,e2;
   /*/@ invariant \typeof(etatCourant)==\type(E0) ||
                          \typeof(etatCourant)==\type(E1) || 
                         \typeof(etatCourant)==\type(E2); */
   //@ invariant etatCourant==e0 || etatCourant==e1 || etatCourant==e2 ;
   //@ invariant \typeof(e0)==\type(E0) & \typeof(e1)==\type(E1) & \typeof(e2)==\type(E2) ;
   //@ invariant e0.etatsSuivants[0] == e1 & e0.etatsSuivants[1] == e2;
   //@ invariant e1.etatsSuivants[0] == e1 & e1.etatsSuivants[1] == e2;
   //@ invariant e2.etatsSuivants[0] == e1 & e2.etatsSuivants[1] == e2;
   //@ invariant (\forall Etat e; e.etatsSuivants.length==2 );
   
   //@ ensures etatCourant==e0;
   public Automate(){






                       }     
   
     //@ also_ensures \old(etatCourant) == e0 && entree == 0 ==> etatCourant == e1
     //@ also_ensures \old(etatCourant) == e0 && entree == 1 ==> etatCourant == e2; 
     //@ also_ensures \old(etatCourant) == e1 && entree == 0 ==> etatCourant == e1;
     //@ also_ensures \old(etatCourant) == e1 && entree == 1 ==> etatCourant == e2;
     //@ also_ensures \old(etatCourant) == e2 && entree == 0 ==> etatCourant == e1;
     //@ also_ensures \old(etatCourant) == e2 && entree == 1 ==> etatCourant == e2;
    public Etat transiter(int entree){
             return super.transiter(entree);
     }

   //@ invariant e0.sortie=='a' & e1.sortie=='b' & e2.sortie=='c';

}

 
abstract class Etat{
        
   protected /*@ spec_public */ char sortie;
   protected /*@ spec_public non_null*/ Etat[] etatsSuivants;
  //@ invariant \nonnullelements(etatsSuivants) && etatsSuivants.length>0;
  
  public Etat(){
     //@ assume \nonnullelements(etatsSuivants)&& etatsSuivants.length>0;
          }
          
  //@ requires \nonnullelements(etatsSuivants) && etatsSuivants.length>0;
  //@ modifies this.etatsSuivants;
  //@ ensures this.etatsSuivants==etatsSuivants;
  public void setEtatsSuivants(Etat[] etatsSuivants){


          }
          
  //@ ensures \result==etatsSuivants;        
  public Etat[] getEtatsSuivants(){


          }
          
  //@ requires i>=0  & i<etatsSuivants.length;
  //@ ensures \result==etatsSuivants[i]; 
  public Etat getEtatsSuivants(int i){


          }

  //Automate de Moore : l'action de sortie est associée à l'état  
  //@ modifies sortie;
  //@ ensures \result==sortie;
   abstract public char action();
  
  //@ requires entree>=0 & entree<etatsSuivants.length;
  //@ ensures \result != null 
  //@ ensures \result==this.etatsSuivants[entree];
  public Etat transiter(int entree){


          }
}


final class E0 extends Etat{
   
   //@ ensures sortie=='a';
   public E0(){


           }
   public char action(){ 


   }

}
 
final class E1 extends Etat{
        
   //@ ensures sortie=='b';
   public E1(){


           } 
   public char action(){ 


   }
}


final class E2 extends Etat{
   //@ ensures sortie=='c';
   public E2(){


           } 
   public char action(){ 


   }
}



public class Application{
    static Automate detecteur;
  //@ requires args[0]=="0" && args[1]=="1" && args[2]=="1"
  //@ ensures detecteur.etatCourant == detecteur.e2; 
  public static void main(String[] args){












  }



// c'est tout… ces 4 pages d'exercice Java sont à rendre avec votre copie d'examen