uv16472

Soit les affirmations :

1- les programmeurs sont droitiers ou intelligents

2- aucun programmeur intelligent ne programme sans "SPEC"

3- mais il y a des programmeurs qui programment sans "SPEC" et sans analyse

Alors on peut conclure qu'il y a des programmeurs droitiers qui programment sans analyse !…

Question 1.1 : formaliser ces affirmations et la conclusion dans des formules logiques.

Remarque : penser aux formes aristotéliciennes pour la "traduction"

Question 1.2 : Démontrer cette énigme par les tableaux sémantiques.

Exemples :

a v (b & ~c) s'écrit <bool><ou> a <et> b <non>c</non></et></ou></bool>

~(a v b) & c s'écrit <bool><et><non><ou> a b</ou></non> c</et></bool>

Soit une syntaxe abstraite pour ces formules :

1) Catégories syntaxiques :

f , f1 , ... : F (formule booléenne)

e , e1 , ... : E (Expression booléeene)

b , b1 , ... [vrai , faux]

v , v1 , .. [a,b,c,d]

2) Définitions :

f ::= <bool> e </bool>

e ::= <et> e1 e2 </et> | <ou> e1 e2 </ou> | <non> e1 </non>| b | v

QUESTION : Donnez les règles d'inférence pour l'évaluation de ces expressions.

Remarques :

-Ce ne sont pas les règles en Prolog qui sont demandées ici (cf. ci-dessous).

-Les variables sont associées à une valeur booléenne {vrai , faux} dans un contexte.

-Ce contexte doit être présent dans chaque règle.

Comme dans la question 2, on dispose d'expressions booléennes sur les opérateurs & , v et ~et les 4 variables a,b,c,d sous une forme " XML-Style ". Exemples :

a v (b & ~c) s'écrit maintenant en Prolog :

['<bool>' , '<ou>' , a ,'<et>' , b , '<non>', c ,'</non>','</et>','</ou>','</bool>']

~(a v b) & c s'écrit maintenant en Prolog :

[ '<bool>' , '<et>' , '<non>' , '<ou>' , a , b , '</ou>' , '</non>' , c , '</et>' , '</bool>]

Cette fois on choisit de " valider " d'abord les expressions avant de les éditer et de les évaluer.

Pour les valider on utilise la DCG suivante :

f --> ['<bool>' ] , e , ['</bool>'].

e --> ['<et>' ] , e , e , ['</et>'].

e --> ['<ou>' ] , e , e , ['</ou>'].

e --> ['<non>' ] , e , ['</non>'].

e --> [X] , {member(X , [vrai , faux , a , b , c , d])}.

QUESTION 3.1 : Augmenter cette grammaire pour reconstruire la forme standard des expressions au cours de l'analyse.

Remarques : on a déclaré les opérateurs :

:- op(603 , xfy , &).

:- op(603 , xfy , v).

:- op(601 , fy , ~).

Exemple :

?- f(AST , ['<bool>','<ou>',a,'<et>',b ,'<non>',c ,'</non>','</et>','</ou>','</bool>'] , []).

AST= a v b & ~c

Pour évaluer l'expression, on a vu qu'il faut disposer d'un contexte qui contient l'assignation sémantique des variables de l'expression. On choisit, en Prolog de représenter ce contexte par par une liste d'égalités. Exemple : [a=vrai , d=faux , b=vrai]. Ce contexte est introduit dans la grammaire :

f(CTX) --> ['<bool>' ] , e(CTX) , ['</bool>'].

e(CTX) --> ['<et>' ] , e(CTX) , e(CTX) , ['</et>'].

e(CTX) --> ['<ou>' ] , e(CTX) , e(CTX) , ['</ou>'].

e(CTX) --> ['<non>' ] , e(CTX) , ['</non>'].

e(CTX) --> [X] , {member(X , [vrai , faux ])}.

e(CTX) --> [X] , {member(X , [a , b , c , d])}.

QUESTION 3.2 : Augmenter cette grammaire pour reconstruire la forme standard des expressions ET les évaluer au cours de l'analyse.

Remarques : pour l'évaluation on a besoin des tables :

non(vrai , faux).

non(faux , vrai).

4-Java :

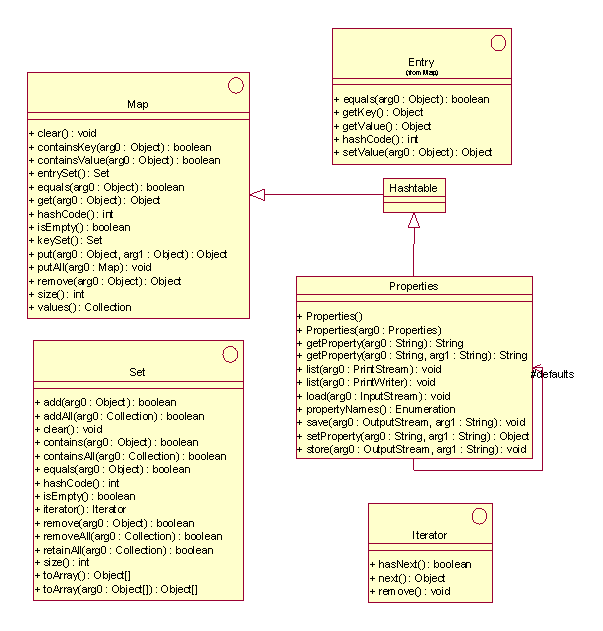
L'objectif est de programmer une implantation de l'interface Iterator, spécifiée dans Java par :

	Java.util Interface Iterator{
		boolean hasNext(); // retourne true si l'itération a encore des éléments.
		Object next(); // retourne l'élément suivant dans l'itération.
		void remove(); // qui ne sera pas implantée ici.
	}

Question 4.1 : l'implantation qui vous est demandée a pour but de filtrer dans une énumération d'objets ceux qui sont des nombres.

Ci dessous un exemple de déclaration et d'usage d'une instance de la classe FilterNumber qui est à développer :

import java.util.*;
public class IterIterator {
	public static void main(String args[]) {
		// créer une liste
		List list = new ArrayList();
		// lui ajouter des éléments de différents types
		list.add(null);	list.add("test1");
		list.add(new Integer(37));	list.add(new Double(12.34));
	        list.add(null);	list.add("test2");
		list.add(new Long(12345));	list.add(null);
		list.add(new Byte((byte)125));
		// filtrer et afficher les seuls elements de classe Number
		Iterator iter = new FilterNumbers( list.iterator());
		 while (iter.hasNext())  System.out.println(iter.next());
	}
}

Pour énumérer les seuls éléments numériques de notre liste, on souhaite donc disposer d'un filtre numérique qui soit un itérateur sur les éléments de la liste, eux même obtenus par l'iterator fourni par l'instance d'ArrayList…

Schéma du programme demandé : 
import java.util.*;
class FilterNumbers implements Iterator {
	private final Iterator iter;
	private Object nextnum;
	public FilterNumbers(Iterator iter) {
		…
	}

	public boolean hasNext() {
	//retourne true si il existe encore un objet instance de Number 
		…
	}

	public Object next() {
	// retourne le prochain objet instance de Number,
	// sinon lève l'exception NoSuchElementException.
		…
	}

	public void remove() {
		throw new UnsupportedOperationException();
	}
}
L'exécution du programme donne : 
	37
	12.34
	12345
	125

Question 4.2 : On demande de généraliser de sorte que le filtre s'applique à tout type de classe (classe Class) passée en paramètre au constructeur du filtre.