uv16472

Vérifier par les tableaux sémantiques ou le calcul des séquents que ~ 'E'(x , y)(cube(x) &cube(y) & aGauche(y , x)) est conséquence logique des prémisses suivantes :

(i) 'A' (x , y)(aGauche(x , y) -> plusGrand(x , y))

(ii) 'A' (x)(cube(x) -> petit(x ))

(iii) 'A' (x)(tétraèdre(x) -> petit(x ))

(iv) 'A' (x , y)(( petit(x) & petit(y))-> ~plusGrand(x , y))

étudiant(<NOM> , <MATRICULE> , <LISTE de NOTES>).

Une note est un terme : dh(<NUMERO DH> , <NOTE>).

Exemple :

étudiant(et1 , i12345 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et5 , i12349 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et2 , i12346 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et3 , i12347 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et4 , i12348 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et6 , i12350 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 0) ]).

étudiant(et71 , i12351 , [dh(1 , 5) , dh(2 , 3) , dh(4 , 2) , dh(8 , 5) , dh(3 , 5) ]).

Remarque : ici, les DH sont tous notés sur 5.

On obtient la liste des étudiants (plus facile à manipuler) simplement par :

listeEtudiants(L) :- setof(étudiant(N , M , DH) , étudiant(N , M , DH) , L).

exemple en reprenant l'exemple ci dessus :

?- listeEtudiants(L) .

L = [étudiant(et1, i12345, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et5, i12349, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et2, i12346, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et3, i12347, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et4, i12348, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et6, i12350, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 0)]), étudiant(et71, i12351, [dh(1, 5), dh(2, 3), dh(4, 2), dh(8, 5), dh(3, 5)])]

Les règles de calcul du bonus sont :

1 point pour au moins 10 DH rendus avec une note > 0

2 points pour au moins 8 DH rendus avec une note > 2

3 points pour au moins 9 DH rendus avec une note > 2 dont 4 avec la note 5

0 point dans tous les autres cas.

Alors on ajoute 3 paramètres aux termes étudiant/3 , les 3 champs <Nb SUP0> , <Nb SUP2> , <Nb MAX> , soient le nombre de DH rendus avec une note >0 , le nombre de DH rendus avec une note >2 , le nombre de DH rendus avec la note 5

Donc on a maintenant

étudiant(<NOM>,<MAT>,<NOTES>,<Nb SUP0>,<Nb SUP2>,<Nb MAX>).

La nouvelle liste d'étudiants est obtenue par :

listeEtudiantsRendusSup2MAX([] , []).

listeEtudiantsRendusSup2MAX([étudiant(N , M , DH) | L] , [étudiant(N , M , DH , Rendus , SUP2 , MAX) | L1]) :-

      sansZero(DH , DH1) , length(DH1 , Rendus),

      sup2(DH1 , DH2) , length(DH2 , SUP2),

      max(DH2 , DH3) , length(DH3 , MAX),

      listeEtudiantsRendusSup2MAX(L ,L1).

sansZero([] , []) .

sansZero([dh(_ , Note) | L] , L1) :- compare(= , Note , 0) , sansZero(L , L1).

sansZero([dh(Nu , Note) | L] , [dh(Nu , Note) | L1]) :- compare(> , Note , 0) , sansZero(L , L1).

sup2([] , []) .

sup2([dh(_ , Note) | L] , L1) :- compare(< , Note , 3) , sup2(L , L1).

sup2([dh(Nu , Note) | L] , [dh(Nu , Note) | L1]) :- compare(> , Note , 2) , sup2(L , L1).

max([] , []) .

max([dh(_ , Note) | L] , L1) :- compare(< , Note , 5) , max(L , L1).

max([dh(Nu , Note) | L] , [dh(Nu , Note) | L1]) :-  compare(= , Note , 5) , max(L , L1).

Rappel : compare(?Order, +Term1, +Term2) : Détermine ou teste l'Order entre 2 termes dans l'ordre standard

des termes. Order peut prendre les valeurs <, > ou =.

QUESTION : Ajouter au programme Prolog ci dessus la procédure Prolog qui retourne la liste des bonus selon les règles fixées.

listeBONUS(LISTEBONUS) :- /* à completer */

LISTEBONUS est donc une liste de termes de la forme : bonus(<NOM> , <MATRICULE> , <BONUS>).

le premier exemple donné dans ESC/JAVA est Bag.java. Complètement documenté en ESCJAVA on obtient :

class Bag {       /*@ non_null */ int[] a;       int n;       //@ invariant 0 <= n && n <= a.length;       //@ requires input != null && input.length>=1;       //@ensures n==a.length;       //@ensures (\forall int k; k>=0 && k<input.length ==> input[k]==a[k]);       Bag(int[] input) {             n = input.length;             a = new int[n];             System.arraycopy(input, 0, a, 0, n);       }       //@ requires n >= 1;       //@ensures (\forall int k; k>=0 && k<n ==> \result<=a[k]);       int extractMin() {             int m = Integer.MAX_VALUE;             //@assume (\forall int k; k>=0 && k<n ==> a[k]<m);             int mindex = 0;             /*@ loop_invariant (\forall int k; k>=0 && k<i ==> m<=a[k]) && 0 <= mindex && mindex <= i && i>=0 && i<=n;*/             //@decreases n-i;             for (int i = 0; i < n; i++) {                   if (a[i] < m) {mindex = i; m = a[i]; }             }             /*@assert (\forall int k; k>=0 && k<n ==> m<=a[k]) && 0 <= mindex && mindex <= n;*/             n--;             a[mindex] = a[n];             //@assert (\forall int k; k>=0 && k<n ==> m<=a[k]);             return m;       } }

QUESTION1 : Reprendre le corps de la méthode extractMin() y compris les commentaires ESC/JAVA, pour le réécrire selon le formalisme de la logique de HOARE et en transformant la boucle "for" en une boucle "while".

Remarque : la formule ('A' k : k>=0 & k<i ==> m<=a[k]) est considérée comme vraie " par défaut " quand i=0 (puisqu'il n'existe pas de k donc de a[k]

QUESTION2 : Enoncer toutes les obligations de preuves pour prouver la boucle " while " obtenue. (ATTENTION : les démonstrations ne sont pas demandées ici…)

QUESTION3 : établir la preuve de la terminaison de la boucle (le point 5 du canevas)

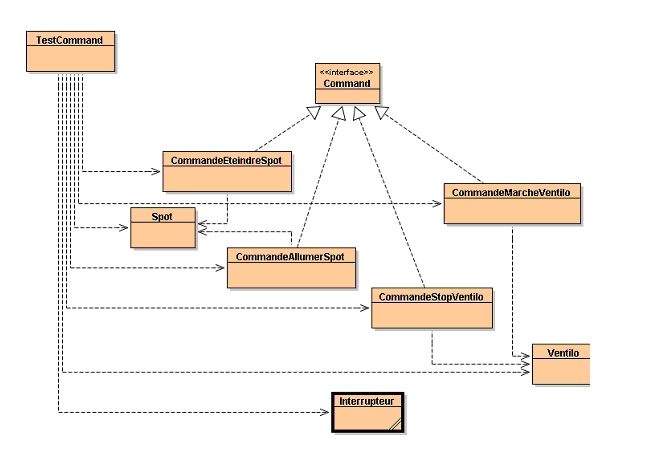
4-Java (5 points) :  Pattern Commande

Le langage java ne permet pas de passer une procédure en paramètre ou de l'affecter à une variable pour réaliser l'équivalent d'un 'callback'. Pour affecter à différentes structures de commande des fonctions différentes on peut utiliser le pattern dit 'pattern Command'. L'interface ci-dessous

public interface Command {
        public abstract void execute ( );
}

peut donc être implémenté par des classes concrètes, la méthode execute étant spécialisée en conséquence. Différents objets de CommandeConcrète peuvent alors être affectés à des Boutons ou des interrupteurs conçus pour recevoir des commandes et en lancer l'exécution. Dans l'exemple ci-dessous on souhaite piloter indifféremment à partir d'un interrupteur général, un ventilateur ou un 'spot' lumineux par exemple.

class Ventilo {
        public void start () {
                System.out.println("Ventilo is rotating");
        }
        public void stop () {
                System.out.println("Ventilo is not rotating");
        }
}



class Spot {
        public void turnOn( ) {
                System.out.println("Spot est allumé ");
        }
        public void turnOff( ) {
                System.out.println("Spot est éteint");
        }
}
class Interrupteur {
        private Command UpCommand, DownCommand;
        public Interrupteur( Command Up, Command Down) {
                UpCommand = Up;
                DownCommand = Down;
        }
        void flipUp( ) { 
                        UpCommand . execute ( ) ;

        }
        void flipDown( ) {
                        DownCommand . execute ( );
        }
}

QUESTION : On demande de programmer les différentes classes de commandes concrètes représentées sur la diagramme UML ci-dessus Ainsi que le test qui déclare et pilote deux interrupteurs associés respectivement à un spot et à un ventilateur.

public class TestCommand {
                public static void main(String[] args) {
		….
	   }
}