CDL_B3  uv 16472   Examen première session 1999

Soient les hypothèses  : 
(1)		 x ( Cube(x)  v Pyramide(x) )
(2)		 x ( Cube(x)  ->  Large(x) )
(3)	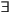	( x ¬ (Large(x) ))

Q1 : montrer par les tableaux sémantiques ou le calcul des séquents que :
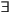		 x ( Pyramide(x) )

2-Prolog, Sémantique structurelle : 
Soient les formules du calcul des propositions sur les opérateurs & (et) , v (ou) et ~ (négation) et des propositions (atomes Prolog). 
Exemple de formule  : (a v b v c) & ~a & (g v a) 
Remarque : les opérateurs & et v sont associatifs et on écrit par exemple 
a & z & e plutot que (a & ( z & e)).
Alors on vise une syntaxe abstraite des formules profitant de l'associativité i.e. une syntaxe abstraite dans laquelle les opérateurs & et v sont d'arité quelconque (supérieure ou égale à 2) i.e. on écrit  et(a,z,e) pour l'exemple précédent.
Soit cette syntaxe abstraite :
Catégories syntaxiques :
	f , f1 , f2 , ... : Formules
	n , n1 , n2 , ... : Négation
	c , c1 , c2 , ... : Conjonction
	d , d1 , d2 , ... : Disjonction
	a , a1 , a2 , ... : Proposition
        lt, lt1, lt2, ... : ListeDeFormules
Définitions : 
	f ::= a | n | c | d
	n ::= negation(f)
	c ::= et(lt)
	d ::= ou(lt)
	lt ::= f1 ',' ( f2 | lt)

Q2.1 : Exprimer dans cette syntaxe abstraite
			(a v b v c) & ~ a & (g v a )

Q2.2 : A partir de formules exprimées dans cette syntaxe abstraite, donner les règles d'inférences de sémantique structurelle ET leurs équivalents Prolog pour l'édition des formules sous leur forme d'origine.
Remarque : en Prolog le prédicat de transformation sera nommé : 
toString/1  (prédicat de nom  toString  d'arité 1)

Q2.3 : Donner la question prolog pour l'édition de la formule obtenue en Q2.1 

  

3-DCG : Une DCG des formules de la question 2 est la suivante : 

formule  --> proposition.
formule  --> negation.
formule  --> conjonction.
formule  --> disjonction.
formule  --> ['('] , formule , [')'].

negation --> [~] , proposition.
negation --> [~] , ['('] , formule , [')'].

conjonction  --> membreGauche , [ & ] , conjonction.
conjonction  --> membreGauche , [ & ] , nonConjonction.

disjonction  --> membreGauche , [ v ] , disjonction.
disjonction  --> membreGauche , [ v ] , nonDisjonction.

proposition -->
	[A] , {atom(A) , not member(A , ['(',')',[],&,~,v ])}.

membreGauche  --> proposition.
membreGauche  --> negation.
membreGauche  --> ['('] , formule , [')'].

nonDisjonction  --> negation.
nonDisjonction  --> conjonction.
nonDisjonction  --> proposition.
nonDisjonction  --> ['('] , formule , [')'].

nonConjonction  --> negation.
nonConjonction  --> disjonction.
nonConjonction  --> proposition.
nonConjonction  --> ['('] , formule , [')'].


Q3.1 : Donner la question pour l'analyse de la formule : 
		(a v b v c) & ~a & g v a

Remarque : la DCG qui précède est adaptée à la génération des formules exprimées dans la syntaxe abstraite de la question 2

Q3.2 : Augmenter la DCG pour construire l'arbre de syntaxe abstraite des formules selon la syntaxe abstraite de la question 2.

4-Java :
Les formules propositionnelles en Java utilisent la hiérarchie de classes suivante : 
En notation UML :

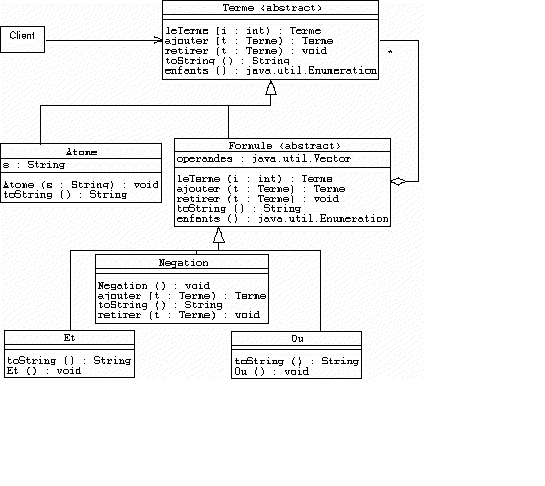Commentaires : Cette organisation est inspirée du "pattern Composite"
La classe abstraite "Terme" est utilisée par le programme Client. 
Une formule propositionnelle est un Terme (Formule extends Terme).
La conjonction de termes est une formule (Et extends Formule), ainsi que la disjonction (Ou extends Formule).
Les formules en Et et en Ou ont en argument des termes et sont d'arité quelconque.
La négation est également une formule (Negation extends Formule), son arité est 1.
Les propositions sont les symboles terminaux d'une formule, ce sont des atomes (Atome extends Terme).

Ci-dessous un exemple de Source Java extrait d'un Client de la classe Terme,

try{
	Terme termeEt = new Et().ajouter(new Atome("b")).ajouter(
					new Atome("c")).ajouter(new Atome("e"));
	Terme termeNeg = new Negation().ajouter(termeEt);
	Terme termeOu = new Ou().ajouter(
					new Atome("a")).ajouter(termeNeg);

	System.out.println(" s = " + termeOu.toString());
		// affiche s = (a v ~((b & c & e)))
	System.out.println(new Negation().ajouter(termeNeg));
		// affiche ~(~((b & c & e)))
	termeNeg.ajouter(new Atome("f"));
		// levee d'exception, la negation est d'arite 1 
		// affiche exception de type NonSupporteeException  
	}catch(NonSupporteeException e){
		System.out.println("exception : NonSupporteeException");
	}


Q4-1 : On demande l'implémentation complète de la classe Atome.
 
Q4-2 : On demande l'implémentation de la méthode "String toString()" des classes Et et Negation. 

Q4-3 : On demande l'implémentation de la classe abstraite Formule.

Remarque : La classe Formule possède l'attribut Operandes de classe java.util.Vector.

On rappelle que la classe Vector définit en particulier les méthodes suivantes : 

public Vector();
public void addElement(Object o);
public  Object elementAt(int index)
			throws ArrayIndexOutOfBoundsException;
public boolean removeElement(Object o);
public int size();

  

c'est tout pour juin 1999

/* une idée de ce qui était attendu......