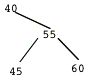CorrigÈ de lπexamen de Structures de donnÈes du 8 fÈvrier 2003

Exercice 1

Question A

Un arbre AVL est un arbre binaire de recherche qui est H-ÈquilibrÈ. Un arbre binaire de recherche est tel que la clÈ de tout n¶ud est plus grande que toutes les clÈs des n¶uds de son sous arbre gauche et plus petite que toutes les clÈs des n¶uds de son sous arbre droit. Un arbre binaire est H-ÈquilibrÈ si en tout n¶ud, la diffÈrence de hauteur entre les sous arbres gauche et droit est au plus de 1. On peut constater sur lπarbre donnÈ quπil sπagit bien dπun arbre binaire de recherche, et que de plus il est H-ÈquilibrÈ. On peut le dÈcorer avec les dÈsÈquilibres (-, =, +).

Question B

Lπadjonction dans un arbre AVL consiste dπabord ‡ faire une adjonction dπune feuille dans un arbre binaire de recherche, en recherchant lπendroit o˘ doit Ítre le n¶ud en tant que feuille. Pour cela, partant de la racine, on descend dans lπarbre, ‡ gauche ou ‡ droite, selon que la clÈ de lπÈlÈment ajoutÈ est infÈrieure ou supÈrieure ‡ la clÈ du n¶ud, jusquπ‡ rencontrer un arbre vide qui est remplacÈ par un nouveau n¶ud contenant lπÈlÈment ajoutÈ. Ensuite, on remonte le chemin vers la racine, en corrigeant les dÈsÈquilibres (+1 si on remonte depuis la gauche et ≠1 si on remonte depuis la droite), en vÈrifiant que le rÈsultat reste dans les limites (-1, 0 ou +1) et en pratiquant la rotation adaptÈe si ce nπest pas le cas. Dans tous les cas, on arrÍte la remontÈe et les corrections lorsque le dÈsÈquilibre rÈsultant est nul.

Question C

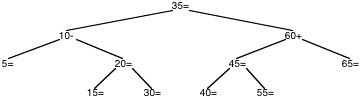
On part de lπarbre ci-dessus, pour ajouter dπabord 50. 50 Ètant plus grand que 35, on descend ‡ droite. 50 Ètant plus petit que 60 on descend ‡ gauche. 50 est plus grand que 45 on descend ‡ droite. 50 est plus petit que 55 on descend ‡ gauche. On est sur un arbre vide qui est donc remplacÈ par le n¶ud 50, fils gauche de 55. Ceci porte le dÈsÈquilibre de 55 ‡ +1, celui de 45 ‡ ≠1, et celui de 60 ‡ +2. Il faut alors pratiquer une rotation gauche-droite puisque le dÈsÈquilibre de 45 est ≠1. Ceci met 55 ‡ la place de 60 avec un dÈsÈquilibre nul ; la remontÈe est donc terminÈe, et on obtient lπarbre ci-dessous.

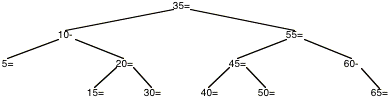
Pour ajouter 25 dans ce nouvel arbre, 25 Ètant plus petit que 35, on descend ‡ gauche. 25 Ètant plus grand que 10 on descend ‡ droite. 25 Ètant plus grand que 20 on descend ‡ droite. 25 Ètant plus petit que 30 on descend ‡ gauche. On est sur un arbre vide qui est donc remplacÈ par le n¶ud 25, fils gauche de 30. Ceci porte le dÈsÈquilibre de 30 ‡ +1, celui de 20 ‡ ≠1 et celui de 10 ‡ ≠2. Il faut alors pratiquer une rotation ‡ gauche puisque le dÈsÈquilibre de 30 est ≠1. Ceci met 20 ‡ la place de 10 avec un dÈsÈquilibre nul ; la remontÈe est terminÈe et on obtient lπarbre ci-dessous.

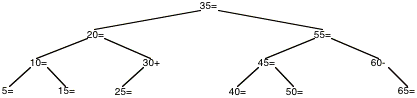
Question D

La liste infixÈe de lπarbre initial est obtenu en mettant chaque n¶ud aprËs la liste infixÈe de son sous arbre gauche et avant la liste infixÈe de son sous arbre droit. On obtient la liste ci-dessous, qui est ordonnÈe pour un arbre binaire de recherche.

5, 10, 15, 20, 30, 35, 40, 45, 55, 60, 65

Question E

LπopÈration de suppression consiste dπabord ‡ rechercher le n¶ud ‡ supprimer. Pour cela, partant de la racine, on descend dans lπarbre, ‡ gauche ou ‡ droite, selon que la clÈ de lπÈlÈment recherchÈ est infÈrieure ou supÈrieure ‡ la clÈ du n¶ud, jusquπ‡ trouver le n¶ud. Si ce n¶ud a deux fils, on remplace la valeur par celle qui est ‡ lπextrÈmitÈ du bord gauche du sous arbre droit, et cπest ce dernier n¶ud qui est supprimÈ. La suppression du n¶ud consiste ensuite ‡ raccrocher le sous arbre Èventuellement existant (gauche ou droit) ‡ sa place. Ensuite, on remonte le chemin vers la racine, en corrigeant les dÈsÈquilibres (-1 si on remonte depuis la gauche et +1 si on remonte depuis la droite), en vÈrifiant que le rÈsultat reste dans les limites (-1, 0 ou +1) et en pratiquant la rotation adaptÈe si ce nπest pas le cas. Dans tous les cas, on arrÍte la remontÈe et les corrections lorsque le dÈsÈquilibre rÈsultant est non nul.

Question F

La suppression de 20 dans lπarbre donnÈ, consiste dπabord ‡ le rechercher. 20 Ètant plus petit que 25, on descend ‡ gauche. 20 Ètant plus grand que 15 on descend ‡ droite. On est alors sur le n¶ud, qui est simplement supprimÈ, puisquπil nπa pas de fils. Le dÈsÈquilibre de 15 devient +2, ce qui nÈcessite une rotation ‡ droite puisque le dÈsÈquilibre de 10 est +1. Le dÈsÈquilibre rÈsultant Ètant nul, il faut poursuivre la remontÈe. Le dÈsÈquilibre de 25 devient ≠2, ce qui demande une rotation ‡ gauche puisque le dÈsÈquilibre de 40 est ≠1. On obtient ainsi lπarbre suivant.

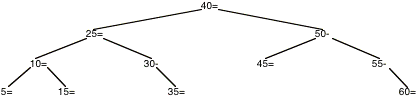
Question G

La suppression de 40 dans lπarbre donnÈ, consiste dπabord ‡ le rechercher. 40 Ètant plus grand que 25, on descend ‡ droite. On est sur le n¶ud qui a deux fils. On remplace la valeur par celle situÈe ‡ lπextrÈmitÈ du bord gauche du sous arbre droit, cπest-‡-dire, 45, et on supprime ce n¶ud. Le dÈsÈquilibre de 50 devient ≠2, ce qui nÈcessite une rotation ‡ gauche, puisque le dÈsÈquilibre de 55 est ≠1. Le dÈsÈquilibre rÈsultant Ètant nul, il faut poursuivre la remontÈe. Le dÈsÈquilibre de 45 devient nul, et celui de 25 Ègalement. Comme on est ‡ la racine, on sπarrÍte.

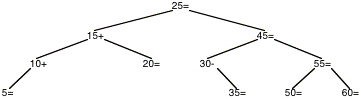
Exercice 2

Question A

En fait lπopÈration de recherche proposÈe ici est analogue ‡ la recherche si une liste est une sous liste dπune autre avec en plus lπinformation sur la position o˘ se trouve cette sous liste. On peut donc sπinspirer de lπexercice correspondant (cf. 15.7 du livre).

Question A.1

Lors de lπappel de Recherche (De => L2, Dans => L1), on va donc comparer les 3 ÈlÈments de la liste L2 avec les portions de la liste L1 de mÍme longueur, et commencant en 1, puis 2, puis 3, etc. jusque 8, o˘ lπon constatera lπÈgalitÈ. La valeur retournÈe sera donc 8.

Lors de lπappel de Recherche (De => L3, Dans => L1), on va donc comparer les 4 ÈlÈments de la liste L3 avec les portions de la liste L1 de mÍme longueur, et commencant en 1, puis 2, puis 3, etc. jusque 10, (ou 13 Èventuellement). A chaque fois, on constatera lπinÈgalitÈ, et donc ‡ la fin lπexception Erreur_Specification sera levÈe. Il est certain que la chaÓne ´ SFIO ª est bien dans le tableau de la liste L1, mais elle est au del‡ de la fin de la liste, donc elle ne fait pas partie de la liste.

Question A.2

On va faire une fonction interne qui contrÙle lπÈgalitÈ de la liste De avec la portion de la sous liste Dans commencant en position En.

function Recherche (De, Dans: Texte) return Positive is
    function Egalite (Decalage: Natural) return Boolean is
    begin
        for I in 1..Longueur (De) loop
            if Ieme (De, I) /= Ieme (Dans, I + Decalage) then
                return False ;
            end if ;
        end loop ;
        return True ;
    end Egalite ;
    for J in 0..Longueur (Dans) ≠ Longueur (De) loop
        if Egalite (J) then return 1 + J; end if ;
    end loop ;
    raise Erreur_Specification ;
end Recherche ;

Soient n la longueur de la liste De et m la longueur de la liste Dans.

1.  Si De est sous liste de Dans, au mieux on le constatera au premier appel de Egalite. Il y aura alors n comparaisons. Au pire, on le constatera ‡ la fin, cπest-‡-dire lors du (m-n+1)Ëme appel de Egalite, les prÈcÈdents ayant ÈchouÈs. La complexitÈ au pire est donc en Q(n*(m-n)). En moyenne, on peut dire quπil y a (m-n)/2 appels de Egalite, chacun dπeux demandant n/2 comparaisons, donnant une complexitÈ en moyenne de Q(n*(m-n)).

2.  Si De nπest pas dans Dans, il faudra appliquer Egalite (m-n) fois. Chacun de ces appels demande au mieux 1 comparaison, au pire n, et en moyenne n/2.

On constate donc que cet algorithme a une complexitÈ en moyenne et au pire en Q(n*(m-n)).

Question B

La suppression des espaces qui se suivent est analogue ‡ la procÈdure Unique sur une liste ordonnÈe, lorsquπon supprime un ÈlÈment de la liste lorsquπil est Ègal ‡ celui qui le prÈcËde (cf. exercice 16.3 question A du livre).

Question B.1

Le rÈsultat de Supprimer_Les_Espaces_Inutiles (L1) est sans effet sur la liste L1. En effet, dans la portion du tableau qui est la reprÈsentation de la liste, il nπy a pas deux espaces qui se suivent. Le seul endroit du tableau o˘ ceci se prÈsente est en dehors de la liste.

Question B.2

Deux mÈthodes peuvent Ítre envisagÈes. La premiËre, simple, utilise lπopÈration Supprimer des listes. Elle a lπinconvÈnient dπÍtre en Q(n²), en particulier si le texte ne contient que des espaces ! La seconde est un peu plus compliquÈe. Il sπagit de dÈplacer les ÈlÈments de la liste lorsque lπon connaÓt leur place dÈfinitive. Sa complexitÈ est alors en Q(n). Nous ne donnons que cette version dans ce corrigÈ.

procedure Supprimer_Les_Espaces_Inutiles
                             (Dans: in out Texte) is
    I: Positive := 1;
begin
    if Longueur (Dans) = 0 then return; end if;
    for J in 2..Longueur (Dans) loop
        if Ieme (Dans, J) /= å å
        or else Ieme (Dans, I) /= å å then
            I := I + 1 ;
            if I /= J then
                Changer_Ieme (Dans => Dans, En => I,
                                Val => Ieme (Dans, J)) ;
            end if ;
        end if ;
    end loop ;
    Tronquer (Dans, I) ;
end Supprimer_Les_Espaces_Inutiles ;

Question C

Pour la substitution, il faut dπabord localiser La_chaine dans le texte. Pour cela, on peut utiliser la fonction ÈtudiÈe en A. Ensuite, il faut remplacer la portion de texte par la nouvelle. Celle-ci peut Ítre plus courte ou plus longue que lπancienne, et pour cela il faut dÈplacer les ÈlÈments qui sont derriËre.

Question C.1

Nous avons vu que le texte L2 est en 8 dans L1. Il faut le remplacer par un texte plus long (4 au lieu de 3). Il faut donc dÈplacer la portion derriËre lui et on obtient finalement la liste L1 suivante.

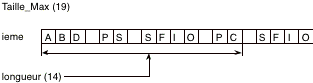
Question C.2

Nous prendrons ici une mÈthode simple. Si le texte de remplacement est plus court que le texte initial, on remplace lπancien par le nouveau et on supprime les ÈlÈments de lπancien qui sont en trop. Si le texte de remplacement est plus long que le texte initial, on remplace la portion de mÍme longueur et on insËre les ÈlÈments restant. Evidemment dans ce contexte, les suppressions un par un ou les insertions un par un sont en p*m o˘ p est le nombre de caractËres au del‡ de la portion remplacÈe et m la diffÈrence de longueur entre les deux textes substituÈs.

procedure Substituer (La_Chaine : in Texte ;
                      Par : in Texte ;
                      Dans : in out Texte) is
    Position : Positive := Recherche (De => La_Chaine,
                                      Dans => Dans) ;
    long: Natural := Longueur(La_Chaine);
begin
    if Longueur(Dans) ≠ long + Longueur(Par)
                                    > Dans.Taille_Max then
        raise Limite_Implantation; -- trop longue
    end if ;
    if long > Longueur (Par) then
        long := Longueur(Par);
        --la plus courte des deux longueurs
    end if;
    -- on repopie dπabord la plus courte des deux longueurs
    for I in 1..long loop
        Changer_Ieme(Dans => Dans, En => Position + I ≠ 1,
                     Val => Ieme (Par, I));
    end loop;
    -- on supprime ceux qui sont en trop, sπil y en a
    for I in long + 1..Longueur (La_Chaine) loop
        Supprimer (Dans, Position + Longueur(Par));
    end loop;
    -- on insËre ceux qui restent, sπil y en a
    for I in long + 1..Longueur(Par) loop
        Inserer (Dans => Dans, En => Position + I - 1,
                 Val => Ieme(Par, I));
    end loop;
end Substituer;

Exercice 0 (QCM)

2       Dans un B-arbre d'ordre 10, qui contient 100 000 valeurs, ‡ combien estimez-vous le nombre dπaccËs disque pour rechercher un ÈlÈment ?

Note ; la hauteur du B-arbre est comprise entre log₂₁100000 et log₁₁50000. Ce ne peut Ítre que 5.

3       Dans un B-arbre d'ordre m, qui contient N valeurs, si on applique une recherche dichotomique sur les n¶uds, combien y aura-t-il de comparaisons ?

Note : voir 12.7 du livre.

4       Si on trie une liste contiguÎ, qui contient 100 000 valeurs, par un tri par tas, sur une machine dont le temps de base dπune comparaison ou dπun transfert est de lπordre de la dizaine de microsecondes, ‡ combien estimez-vous le temps de tri?

Note : la complexitÈ est en n log₂n (2Tc+Tt).

5       Si on trie une liste contiguÎ, qui contient 100 000 valeurs, par un tri par la mÈthode de la bulle, sur une machine dont le temps de base dπune comparaison ou dπun transfert est de lπordre de la dizaine de microsecondes, ‡ combien estimez-vous le temps de tri?

Note : la complexitÈ est en n²/4 (Tc+3Tt).

6       Quel est lπordre de grandeur de la complexitÈ au pire de lπopÈration qui teste si deux arbres binaires de recherche contiennent les mÍmes ÈlÈments, en supposant quπils en contiennent au plus n?

Note : Comme il sπagit dπarbres binaires de recherche, ils contiennent les mÍmes ÈlÈments sπils ont mÍme liste infixe. Donc il faut parcourir les deux arbres selon leur liste infixe et vÈrifier lπÈgalitÈ des contenus n¶ud par n¶ud.

7       Si on dÈfinit dÈbut(x)=cons(premier(x),listevide), parmi les cinq ÈgalitÈs suivantes, quelle est celle qui est obligatoirement vraie?

 concatÈner(dÈbut(x),x)=concatÈner(x,fin(x))
 dÈbut(fin(x))=x
 concatÈner(dÈbut(x),fin(x))=x
 dÈbut(fin(x))=fin(dÈbut(x))
 fin(dÈbut(x))=x

Note : un raisonnement simple sur les longueurs des listes conduit ‡ Èliminer les autres possibilitÈs.

8       Supposons une liste construite ‡ lπaide des types suivants:

    type Place; type Pt_Place is access Place;
    type Place is record
        Contenu: Element;
        Suivant: Pt_Place;
    end record;

Quel groupe dπinstructions implante lπopÈration insÈrer p aprËs q, o˘ q repËre un ÈlÈment de la liste et p repËre lπÈlÈment ‡ insÈrer?

 Q.Suivant := P.Suivant; P.Suivant := Q;
 P.Suivant := Q; Q.Suivant := P.Suivant;
 P.Suivant := Q.Suivant; Q.Suivant := P;
 Q.Suivant := P; P.Suivant := Q.Suivant;
 Q.Suivant := P.Suivant; P.Suivant := Q.Suivant;

Note : les autres possibilitÈs entraÓnent la perte du contenu initial de Q.Suivant, sans lπavoir conservÈ au prÈalable.

9       Ajouter 45 dans l'arbre binaire de recherche suivant, et expliquer.

10     On dispose dπun fichier de hachage qui contient 100 000 ÈlÈments. Chaque bloc disque peut contenir 40 ÈlÈments. La fonction de hachage a pour rÈsultat un nombre entre 1 et 1000, Èquitablement rÈpartis. A combien estimez-vous le nombre dπaccËs disque pour rechercher un ÈlÈment ?

Note : en moyenne, les listes de hachage contiennent 100 000/1 000 soit 100 ÈlÈments, qui sont donc rÈpartis sur 100/40=2,5 blocs.