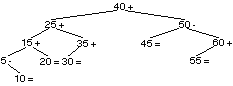Exercice 1 (7 points)
Les quelques déclarations sont précisées
en Ada pour fixer les idées, mais vous pouvez utiliser le langage
de votre choix.
Dans une compétition de sports individuels, les
candidats sont numérotés par ordre d'inscription, et doivent
passer un certain nombre d'épreuves. Pour chacune des épreuves,
ils reçoivent une note qui intervient dans le score final. Nous ne
préciserons pas comment ce score est calculé. Il nous suffit
de savoir que le score est un nombre flottant positif ou nul (il est nul
si le candidat n'a encore participé à aucune épreuve,
ou n’en a réussi aucune) et que, lors de chacune des épreuves,
un nouveau score lui est attribué qui peut être meilleur ou
moins bon que son score précédent.
On désire conserver les informations dans une structure
de données qui permette:
- d'ajouter un candidat lors de son inscription,
- de modifier le score d'un candidat,
- de savoir à tout instant quels sont les
trois meilleurs candidats, c'est-à-dire ceux dont le score est
le plus élevé,
- de connaître pour tout candidat inscrit
quelle est sa position dans le classement de tous les concurrents.
On prend une liste contiguë
dont les éléments sont constitués du numéro
du candidat et de son score. La déclaration Ada de cette liste, appelée
L_SCORE, pourrait
être la suivante:
type Candidat is
record
Numero : Positive;
Score : Float := 0.0;
end record;
package PLC is new Listes_Contigues (Candidat);
L_Score : PLC.Liste (1000);
-- la liste L_Score est une liste contiguë d’au plus
-- 1000 éléments de type Candidat
A(1 pt.)- Définissez l’ordre dans lequel
vous choisissez de mettre les éléments dans la liste, en justifiant
votre choix.
B(1 pt.)- Proposer la procédure qui attribue
un numéro à un candidat lors de son inscription et l'ajoute
à la liste. Évaluer la complexité. La spécification
Ada pourrait être:
procedure Nouveau_Candidat (N : out Positive);
C(1 pt.)- Proposer la fonction qui retourne la place
actuelle dans la compétition d'un candidat dont on connaît
le numéro. Évaluer la complexité. La spécification
Ada pourrait être:
function Position (N : Positive) return Positive;
D(1 pt.)- Proposer la procédure qui modifie
le score d'un candidat. Évaluer la complexité. La spécification
Ada pourrait être:
procedure Nouveau_Score (N : in Positive; S : in Float);
E(1 pt.)- Proposer la fonction qui retourne le numéro
du candidat qui a le score le plus élevé. Évaluer la
complexité. La spécification Ada pourrait être:
function Meilleur return Positive;
F(2 pt.)- Proposer les fonctions qui retournent le
numéro du candidat qui occupe, respectivement, la deuxième
et la troisième place dans la compétition, c'est-à-dire
celui qui a le score le plus élevé après le meilleur
ou après les deux meilleurs. Évaluer la complexité
dans chaque cas. La spécification Ada pourrait être:
function Deuxieme return Positive;
function Troisieme return Positive;
Exercice 2 (4 points)
Dans cet exercice, nous abordons le tri rapide.
A(1 pt.)- Rappeler en quelques lignes le principe
et la complexité du tri rapide.
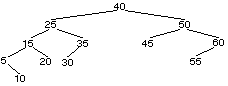
B(3 pts.)- Trier la liste ci-dessous cette méthode.
Vous indiquerez pour chaque grande itération les opérations
effectuées et la liste obtenue.