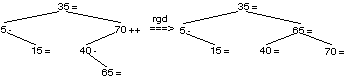
Corrigé de l’examen de Structures de données du 2 février 2002
1 Exercice 1
Nous avons le choix entre 3 ordres possibles : ordre d’arrivée fixe, ordre décroissant des scores et ordre en tas. Nous prenons l’ordre d’arrivée fixe dans ce corrigé.
1.1 Question A
Les éléments sont placés dans la liste au fur et à mesure de l’arrivée des candidats. Aucune propriété n’est supposée sur l’ordre de la liste. Toutes les opérations seront effectuées en parcourant séquentiellement la liste. Évidemment, les opérations relatives au classement des candidats (question C, E, F) pourraient être réalisées avec un tri préalable, mais ce tri devra être refait à chaque fois. Même avec un bon tri, en n log n, ce sera plus coûteux que la réalisation directe de ces opérations par un parcours séquentiel. Par ailleurs, si on ne déplace pas les éléments dans la liste, nous pouvons affirmer qu’un candidat de numéro n est à la place n de la liste, et trouver ainsi immédiatement son score ; les questions C et surtout D en seront facilitées.
1.2 Question B
Il s’agit de mettre le nouvel élément au bout de la liste. La complexité est évidemment indépendante de la longueur de la liste.
procedure Nouveau_Candidat (N : out Positive) is
begin
N := Longueur (L_Score) + 1 ;
Prolonger (L_Score, Val => (N, 0.0)) ;
end Nouveau_Candidat ;
1.3 Question C
Comme indiqué en A, il est facile d’avoir le score du candidat. Il faut ensuite compter combien il y en a qui ont un score supérieur à lui, par un parcours complet de la liste. La complexité est donc proportionnelle à la longueur de la liste.
function Position (N : Positive) return Positive
is
K : Positive := 1 ; -- sa place potentielle
begin
for I in 1..Longueur (L_Score) loop
if Ieme(L_Score, I).Score > Ieme(L_Score, N).Score
then
K := K + 1 ;
end if ;
end loop ;
return K ;
end Position ;
1.4 Question D
Modifier le score d’un candidat est trivial, puisque la place du candidat est donnée par son numéro, et qu’elle ne change pas. La complexité est indépendante de la taille de la liste.
procedure Nouveau_Score (N : in Positive ; S : in Float)
is
begin
Changer_Ieme(L_Score, N, Val => (N, S)) ;
end Nouveau_Score ;
1.5 Question E
Pour trouver le meilleur, il s’agit de trouver l’élément dont le score est le plus grand et de retourner le numéro associé. Il y aurait lieu de prendre garde que la liste ne soit pas vide. Cependant, si ce n’est pas le cas, l’opération Ieme lèvera l’exception Erreur_Specification, ce qui est tout à fait acceptable ici. La complexité est évidemment proportionnelle à la taille de la liste.
function Meilleur return Positive is
K : Positive := 1 ; -- a priori le premier
begin
for I in 2..Longueur (L_Score) loop
if Ieme(L_Score, I).Score > Ieme(L_Score, K).Score
then
K:= I ;
end if
end loop ;
return Ieme(L_Score, K).Numero ;
end Meilleur ;
1.6 Question F
Pour trouver le second, il s’agit de trouver l’élément dont le score est le plus grand après le premier et de retourner le numéro associé. Il y aurait lieu de prendre garde que la liste ne soit pas vide. Cependant, si c’est le cas, l’opération Ieme lèvera l’exception Erreur_Specification, ce qui est tout à fait acceptable ici. La complexité est évidemment proportionnelle à la taille de la liste.
function Deuxieme return Positive is
K : Positive := 1 ; -- a priori le premier
L : Positive := 2 ; -- a priori le second
begin
if Ieme(L_Score, 2).Score > Ieme(L_Score, 1).Score then
K := 2 ; L := 1 ;
end if ;
for I in 3..Longueur (L_Score) loop
if Ieme(L_Score, I).Score > Ieme(L_Score, K).Score
then
L := K ; K := I ;
-- nouveau couple 1-2
elsif Ieme(L_Score, I).Score > Ieme(L_Score,
L).Score then
L := I ; -- nouveau second
end if ;
end loop ;
return Ieme(L_Score, L).Numero ;
end Deuxieme ;
function Troisieme return Positive is
K : Positive := 1 ; -- a priori le premier
L : Positive := 2 ; -- a priori le second
M : Positive := 3 ; -- a priori le troisieme
begin
if Ieme(L_Score, 2).Score > Ieme(L_Score, 1).Score then
K := 2 ; L := 1 ;
end if ;
if Ieme(L_Score, 3).Score > Ieme(L_Score, K).Score then
M := L ; L := K ; M :=
3 ;
elsif Ieme(L_Score, 3).Score > Ieme(L_Score, L).Score then
M := L ; L := 3 ;
else
M := 3 ;
end if ;
for I in 4..Longueur (L_Score) loop
if Ieme(L_Score, I).Score > Ieme(L_Score, K).Score
then
M := L ; L := K ;
K := I ; -- nouveau triplet 1-2-3
elsif Ieme(L_Score, I).Score > Ieme(L_Score,
L).Score then
M := L ; L := I ;
-- nouveau couple 2-3
elsif Ieme(L_Score, I).Score > Ieme(L_Score,
M).Score then
M := I ; -- nouveau troisieme
end if ;
end loop ;
return Ieme(L_Score, M).Numero ;
end Troisieme ;
Remarque
Notons que l’ordre choisi privilégie l’opération Nouveau_Score qui est en Q (1), alors que les opérations Meilleur, Deuxieme et Troisieme sont en Q (n). Intuitivement, si on prend l’ordre décroissant des scores, celles-ci deviendront en Q (1), et Nouveau_Score passera en Q (n). On voit bien que le choix conduit à privilégier certaines opérations par rapport à d’autres.
2 Exercice 2
2.1 Question A
Le tri rapide consiste à partitionner la liste en deux sous listes d’éléments, ceux qui sont inférieurs et ceux qui sont supérieurs à un élément pivot particulier choisi dans la liste, à trier chacune des sous-listes, et à les concaténer. Le choix de cet élément pivot peut être l’élément médian parmi les trois suivants : celui du début de la liste, celui du milieu et celui de la fin.
Pour faire le tri à la place, la valeur pivot provenant de la liste et devant s’y retrouver à la fin, la place qu’elle occcupe dans la liste est une évaluation de celle qu’elle occupera à la fin. On l’appelle la place Presumee. On part de chaque côté de la liste jusqu’à trouver un élément qui n’est pas du bon côté de cette place. Trois cas sont possibles :
2.2 Question B
Dans la suite, nous soulignons les valeurs déplacées au cours d’une étape.
On choisit le pivot, parmi trois valeurs 35 (en 1), 10 (en 7) et 60 (en 14). La valeur médiane est 35. 10 est mis en 1.
|
1 |
choix du pivot (35) |
[10 5 70 15 40 65 — 25 20 30 55 50 45 60] |
|
2 |
échange cas 1 |
[10 5 30 15 40 65 — 25 20 70 55 50 45 60] |
|
3 |
échange cas 1 |
[10 5 30 15 20 65 — 25 40 70 55 50 45 60] |
|
4 |
échange cas 1 |
[10 5 30 15 20 25 — 65 40 70 55 50 45 60] |
|
5 |
listes obtenues |
[10 5 30 15 20 25] 35 [65 40 70 55 50 45 60] |
On continue d’abord sur la liste la plus petite. On choisit le pivot parmi trois valeurs 10 (en 1), 30 (en 3) et 25 (en 6). La valeur médiane est 25. 30 est mis en 6.
|
6 |
choix du pivot (25) |
[10 5 -- 15 20 30] 35 [65 40 70 55 50 45 60] |
|
7 |
échange cas 3 |
[10 5 20 15 -- 30] 35 [65 40 70 55 50 45 60] |
|
8 |
listes obtenues |
[10 5 20 15] 25 [30] 35 [65 40 70 55 50 45 60] |
On continue d’abord sur la liste la plus petite qui ne contient qu’un élément. Elle est donc triée. On reprend la dernière laissée de côté. On choisit le pivot parmi trois valeurs 10 (en 1), 5 (en 2) et 15 (en 4). La valeur médiane est 10. 5 est mis en 1.
|
9 |
choix du pivot (10) |
[5 -- 20 15] 25 [30] 35 [65 40 70 55 50 45 60] |
|
10 |
listes obtenues |
[5] 10 [20 15] 25 [30] 35 [65 40 70 55 50 45 60] |
On continue d’abord sur la liste la plus petite qui ne contient qu’un élément. Elle est donc triée. On reprend la dernière laissée de côté, qui n’en contient que deux. On les ordonne. On reprend la liste restante. On choisit le pivot parmi trois valeurs 65 (en 8), 55 (en 11) et 60 (en 14). La valeur médiane est 60. 55 est mis en 8 et 65 est mis en 14.
|
11 |
ordonner liste de 2 |
[5] 10 [15 20] 25 [30] 35
[65 40 70 55 50 45 60]
|
|
12
|
choix du pivot (60)
|
[5] 10 [15 20] 25 [30] 35 [55 40
70 -- 50 45 65]
|
|
13
|
échange cas 1
|
[5] 10 [15 20] 25 [30] 35 [55 40 45
-- 50 70 65]
|
|
14
|
échange cas 3
|
[5] 10 [15 20] 25 [30] 35 [55 40 45 50
-- 70 65]
|
|
15
|
listes obtenues
|
[5] 10 [15 20] 25 [30] 35 [55 40 45 50]
60 [70 65]
|
On continue d’abord sur la liste la plus petite qui ne contient que deux éléments. On les ordonne. On reprend la liste restante. On choisit le pivot parmi trois valeurs 55 (en 8), 40 (en 9) et 50 (en 11). La valeur médiane est 50. 40 est mis en 8 et 55 est mis en 11.
|
16 |
ordonner liste de 2 |
[5] 10 [15 20] 25 [30] 35 [55 40 45 50] 60 [65 70] |
|
17 |
choix du pivot (50) |
[5] 10 [15 20] 25 [30] 35 [40 -- 45 55] 60 [65 70] |
|
18 |
échange cas 3 |
[5] 10 [15 20] 25 [30] 35 [40 45 -- 55] 60 [65 70] |
|
19 |
listes obtenues |
[5] 10 [15 20] 25 [30] 35 [40 45] 50 [55] 60 [65 70] |
On continue d’abord sur la liste la plus petite qui ne contient qu’un élement ; elle est donc triée. On reprend la dernière qui n’en contient que deux dans le bon ordre. Le tri est donc terminé.
3 Exercice 3
3.1 Question A
3.1.1 Question A.1
Un AVL est arbre binaire de recherche qui est H-équilibré. Un arbre binaire de recherche est un arbre tel que tout nœud a une clé supérieure ou égale à la plus grande clé de son sous-arbre gauche et inférieure ou égale à la plus petite clé de son sous-arbre droit. Un arbre binaire est H-équilibre si, en tout nœud, la différence de hauteur entre le sous-arbre gauche et le sous-arbre droit est au plus de 1.
3.1.2 Question A.2
L’adjonction dans un arbre AVL comporte deux étapes.
3.1.3 Question A.3
On part avec 35. 5 étant plus petit est mis à gauche avec un déséquilibre nul, puis le déséquilibres sur 35 est incrémenté, puisque on remonte depuis la gauche. L’adjonction de 70 doit se faire à droite de 35, qui retrouve un déséquilibre nul. L’adjonction de 15 doit être à gauche de 35, et donc à droite de 5. Le déséquilibre de 5 devient —1, et celui de 35 +1. L’adjonction de 40 doit être à droite de 35, et donc à gauche de 70. Le déséquilibre de 70 devient +1, et celui de 35 redevient nul. L’adjonction de 65 doit être à droite de 35, à gauche de 70, à droite de 40. Le déséquilibre de 40 devient -1, celui de 70 devenant +2. Il faut pratiquer une rotation. Comme le déséquilibre du fils gauche est —1, il s’agit d’une rotation gauche droite.
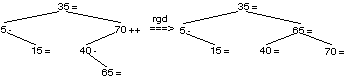
L’adjonction de 10 doit être à gauche de 35, à droite de 5, à gauche de 15. Le déséquilibre de 15 devient +1, et celui de 5 devient —2. Le fils droit de 5 ayant un déséquilibre +1, il faut pratiquer une rotation droite gauche sur 5.
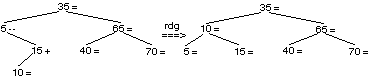
L’adjonction de 25 doit être à gauche de 35, à droite de 10, à droite de 15. Le déséquilibre de 15 devient —1, celui de 10 devient —1 et celui de 35 devient +1. L’adjonction de 20 doit être à gauche de 35, à droite de 10, à droite de 15, à gauche de 25. Le déséquilibre de 25 devient +1 et celui de 15 devient —2. Il faut faire une rotation droite gauche en 15.
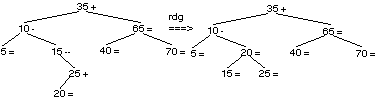
L’adjonction de 30 doit être à gauche de 35, à droite de 10, à droite de 20, à droite de 25. Le déséquilibre de 25 devient —1, celui de 20 devient —1, celui de 10 devient —2. Il faut faire une rotation à droite en 10.
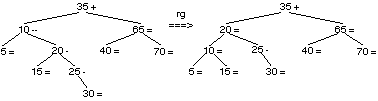
L’adjonction de 55 doit être à droite de 35, à gauche de 65, à droite de 40. Le déséquilibre de 40 devient —1, celui de 65 devient +1 et celui de 35 devient nul. L’adjonction de 50 est à droite de 35, à gauche de 65, à droite de 40 et à gauche de 55. Le déséquilibre de 55 devient +1, et celui de 40 devient —2. Il faut pratiquer une rotation droite gauche en 40.
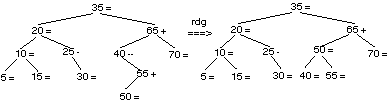
L’adjonction de 45 est à droite de 35, à gauche de 65, à gauche de 50 et à droite de 40. Le déséquilibre de 40 devient -1, celui de 50 devient +1 et celui de 65 devient +2. Il faut pratiquer une rotation à droite en 65.
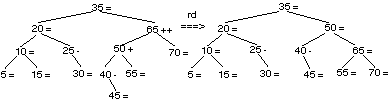
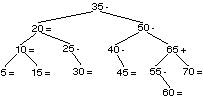
L’adjonction de 60 est à droite de 35, à droite de 50, à gauche de 65, à droite de 55. Le déséquilibre de 55 devient —1, celui de 65 devient +1, celui de 50 devient —1 et celui de 35 devient —1.
3.1.4 Question A.4
La première vérification que l’on peut faire est de constater que la liste infixe de cet arbre est bien la liste triée de celle donnée initialement, puisque ceci est une propriété intrinsèque des arbres bianires de recherche. On peut de plus contrôler que le déséquilibre porté sur l’arbre, à côté de chaque nœud, est bien égal à la hauteur de l’arbre de gauche moins celle de l’arbre de droite, et qu’il est compris entre —1 et +1.
3.2 Question B
3.2.1 Question B.1
La suppression dans un arbre AVL comporte trois étapes.
3.2.2 Question B.2
Le nœud 45 est à droite de 40 et à gauche de 50. Comme il n’a pas de fils, on le remplace par un arbre vide. Le déséquilibre de 50 décrémenté, puisque l’on vient de la gauche. Comme il devient —2, il faut faire une rotation. Comme son fils droit a un déséquilibre +1, il faut faire une rotation droite gauche.
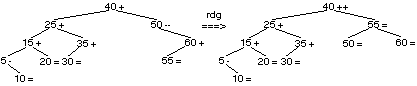
Le déséquilibre résultat sur 55 étant nul, il faut poursuivre et incrémenter celui de 40 qui devient +2. Il faut pratiquer une deuxième rotation, ici à droite, pour terminer la suppression et donner l’arbre de gauche ci-dessous. La suppression de 25 dans ce nouvel arbre, consiste d’abord à remplacer sa valeur par 30, puisqu’il a deux fils. La suppression du fils gauche de 35 remet à 0 son déséquilibre, et porte à -1 celui de 40. Celui-ci étant non nul, il faut arrêter les corrections. L’arbre final est celui de droite.
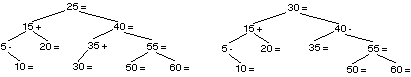
3.3 Question C
3.3.1 Question C.1
La liste préfixe d’un arbre est telle que tout nœud est avant ses descendants, et ceux de son sous-arbre gauche avant ceux de son sous-arbre droit. Pour l’arbre donné, la liste préfixe est :
40, 25, 15, 5, 10, 20, 35, 30, 50, 45, 60, 55
3.3.2 Question C.2
25 est à gauche de 40. 15 est à gauche de 40 et à gauche de 25. 5 est à gauche de 40, à gauche de 25 et à gauche de 15. 10 est à gauche de 40, à gauche de 25, à gauche de 15 et à droite de 5. 20 est à gauche de 40, à gauche de 25 et à droite de 15. 35 est à gauche de 40 et à droite de 25. 30 est à gauche de 40, à droite de 25 et à gauche de 35. 50 est à droite de 40. 45 est à droite de 40 et à gauche de 50. 60 est à droite de 40 et à droite de 60. 55 est à droite de 40, à droite de 50 et à gauche de 60.
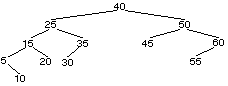
3.3.3 Question C.3
La liste infixe d’un arbre binaire de recherche est une liste ordonnée. On peut donc vérifier que nous avons la liste triée de la liste initiale.
3.3.4 Question C.4
L’arbre binaire de recherche obtenu par adjonction des valeurs aux feuilles, dans l’ordre de la liste préfixe ci-dessus, est le même que celui fourni initialement. En effet, lors de l’adjonction d’un nœud, tous les nœuds ascendants de l’arbre initial le précèdent dans la liste préfixe, et sont donc déjà dans l’arbre que l’on construit. Par contre, ses descendants étant après lui, ne sont pas encore dans l’arbre. En fait, on constate dans la question C.2 que les ascendants constituent le chemin parcouru pour l’adjonction.
Intuitivement, on peut montrer récursivement que le chemin qui mène vers un nœud dans l’arbre reconstruit est le même que celui de l’arbre initial. En effet, lorsque l’on ajoute un nœud dans le nouvel arbre, nous allons parcourir le même chemin depuis la racine jusqu’à son père (hypothèse de récurrence). Si sa place était occupée dans le nouvel arbre, elle ne pourrait l’être que par un de ses descendants de l’arbre initial, or ceux-ci ne sont pas encore ajoutés dans le nouvel arbre. Sa place est donc libre et il est mis au même endroit dans ce nouvel arbre.