2.3. Expressions dans un tableur

Un tableur est un logiciel qui permet la manipulation d'un ensemble de valeurs organisées sous la forme d'un tableau de lignes et de colonnes. Nous considèrerons ici qu'il y a 256 lignes et 256 colonnes. Chaque case du tableau peut contenir soit une chaîne de caractères, soit un nombre, soit une formule. Une formule décrit un calcul qui permet d'obtenir la valeur de la case correspondante. Ce calcul peut utiliser des valeurs d'autres cases du tableau, des nombres ou des fonctions spécifiques prédéfinies. Nous nous intéressons ici à l'analyse lexicale et syntaxique du langage qui permet de définir le contenu d'une case, sous la forme d'une phrase. Ce langage est défini comme suit:
<phrase> ::= <formule> | <nombre signé> | <texte>
<formule> ::= = <expression>
<expression> ::= <terme> {+|-|*|/} <expression> | <terme>
<terme> ::= <référence> | <nombre signé> | ( <expression> )
<nombre signé> ::= <nombre> | {+|-} <nombre>
Un texte est une unité lexicale, constituée d'une suite quelconque de caractères qui n'est pas un nombre signé et qui ne commence pas par le signe "=". Les nombres sont des unités lexicales constituées de chiffres. Les références désignent une case du tableau. Ce sont des unités lexicales constituées d'une ou deux lettres suivies d'un à trois chiffres. Le groupe de lettres repère la colonne (A pour la colonne 1, Z pour la colonne 26, AA pour la colonne 27, AZ pour la colonne 52, etc...) et le groupe de chiffres repère la ligne. Ces unités lexicales peuvent être définies par les règles suivantes, où l'exposant indique le nombre de fois où l'élément correspondant peut être pris:
<nombre> ::= <chiffre> <nombre> | <chiffre>
<référence> ::= {<lettre>}1,2 {<chiffre>}1,3
Les espaces ne peuvent se trouver à l'intérieur d'une unité lexicale, et n'ont pas de signification. Une phrase doit se trouver toute entière sur une seule ligne, et une ligne ne peut contenir qu'une seule phrase.
A- On peut noter qu'un texte est défini par exclusion (toute phrase qui n'est pas lexicalement un nombre et qui ne commence pas par "="). Comment faudra-t-il prendre en compte la règle définissant une phrase?
B- Une référence désigne une case du tableau. Ce tableau contient 256 lignes ou colonnes. Certaines combinaisons conformes à la règle définissant les références ne sont donc pas acceptables. A quel moment doit-on faire le contrôle de la validité d'une référence (lexical, syntaxique ou après)? Justifiez votre raisonnement.
C- On s'intéresse maintenant à l'analyse lexicale des formules. Même si vous savez, évidemment, que l'analyseur lexical fait un codage des différents symboles, nous ne le ferons pas ici pour simplifier. A la place, vous présenterez le découpage en unités lexicales en enfermant celles-ci dans des rectangles.
C.1- Donner le découpage en unités lexicales des phrases suivantes, en justifiant votre raisonnement.
= A11*B2+3
= A2*-5
= 5*(B234-A122)
= A1  2 + B1234
= 23C2
C.2- Que doit indiquer l'analyseur lexical pour les phrases suivantes, en justifiant votre raisonnement.
= AAA2
= A12  $ 45
D- On s'intéresse maintenant à l'analyse syntaxique.
D.1- En vous servant du découpage en unités lexicales fait en C.1, donner la structure syntaxique des phrases suivantes, en justifiant votre raisonnement.
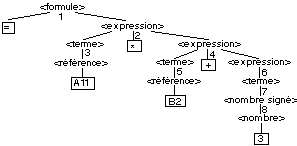
= A11*B2+3
= A2*-5
= 5*(B234-A122)
D.2- En vous servant du découpage en unités lexicales fait en C.1, expliquer pourquoi chacune des phrases suivantes est syntaxiquement erronée.
= A1  2 + B1234
= 23C2
E- L’analyse sémantique consiste à déterminer à partir de l’arbre syntaxique la suite des opérations à effectuer sur les données. On peut simuler ce comportement en faisant les calculs directement sur l’arbre. En supposant que A11 vaut 5, B2 vaut 2, A2 vaut 6, B234 vaut 42 et A122 vaut 38, vous porterez sur chaque nœud des arbres syntaxiques corrects de la question D les valeurs correspondants à ces calculs..
Solution de l’exercice 2.3

2.3.1. Question A

La définition de l'unité lexicale texte présente une certaine forme de dépendance du contexte. Ainsi une suite d'unités lexicales peut être également une unité lexicale texte unique. Par exemple, A23+5, est une suite de 3 unités lexicales si elle est précédée de "=", mais peut aussi être une seule unité lexicale. Ce problème est assez analogue à celui des commentaires dans un langage de programmation. Il est réglé dans ce cas par la présence d'un ou plusieurs caractères précis commençant le commentaire ("--" par exemple en Ada). Il est clair ici que si le premier caractère non espace est "=", il s'agit d'une formule et non d'un texte. De même si ce premier caractère n'est pas un chiffre ni "+", ni "-", alors il s'agit d'un texte. Dans tous les autres cas, le premier caractère ne permet pas de savoir ce qu'il en est. Deux solutions entre autres peuvent être envisagées:
  1. On effectue une analyse lexicale a priori de la phrase complète.
  1. L'autre méthode consiste à contrôler le premier caractère de la phrase.

2.3.2. Question B

L'analyse lexicale d'une référence doit au moins vérifier qu'elle est composée d'une ou deux lettres et de 1 à 3 chiffres. Ce peut être la seule vérification. Il est évident que ZZ ne repère pas une colonne du tableau, bien qu'il n'y ait que deux lettres. De même 342 ne repère pas une ligne du tableau. On peut considérer que cette vérification est d'ordre sémantique, et doit donc être faite ultérieurement. Inversement on peut considérer que cette vérification est d'ordre lexical, et qu'une référence ne peut pas être n'importe quel groupe de deux lettres et n'importe quel groupe de 3 chiffres. La description des groupes acceptables est faisable, mais est assez lourd à faire suivant nos règles habituelles, puisqu'il faudrait lister un grand nombre de cas. Si la règle définissant la structure lexicale d'une référence ne dit pas tout, néanmoins, ZZ342 ne devrait pas être pris lexicalement comme une référence!
Peut-on faire le contrôle au moment de l'analyse lexicale? La réponse est oui, et de façon simple: il suffit de déterminer le numéro de colonne et de ligne durant l'analyse lexicale, en vérifiant que ces numéros sont inférieurs ou égaux à 256. On peut penser d'ailleurs que le codage des unités lexicales reprendrait ce principe.

2.3.3. Question C

2.3.3.1. Question C.1

Les unités lexicales sont constituées des caractères individuels suivants:
= + - * / ( )
ainsi que des nombres et des références.
Le début d'une référence est une lettre alors que le début d'un nombre est un chiffre. Ceci implique que la recherche du début d'une unité lexicale fixera en même temps ce qu'elle peut être. La fin d'un nombre est déterminé par tout caractère différent d'un chiffre. La fin d'une référence est indiquée par un caractère différent d'un chiffre après avoir rencontré au moins un chiffre, ou le fait d'avoir eu 3 chiffres. Evidemment l'absence de chiffres, ou la présence de plus de deux lettres est une erreur lexicale, de même le débordement du numéro de colonne ou de ligne, conformément à ce qui a été dit dans la question B.

La terminaison de la première référence est provoquée par "*", et celle de la seconde est provoquée par "+"

La terminaison de la première référence est provoquée par "*", et celle du nombre est provoquée par la fin de la phrase.

La terminaison de la première référence est provoquée par "-", et celle de la seconde est provoquée par ")".

La terminaison de la première référence est provoquée par l'espace, comme celle du nombre 2. Celle de la deuxième référence est provoquée par la rencontre du troisième chiffre, ce qui implique que le quatrième chiffre commence une nouvelle unité lexicale qui se termine par la fin de la phrase.

La deuxième unité lexicale commence par un chiffre, c'est donc un nombre dont la terminaison est provoquée par la rencontre d'une lettre. Celle-ci commence une nouvelle unité lexicale qui ne peut être qu'une référence qui se termine par la fin de la phrase.

2.3.3.1. Question C.2

Pour la phrase =AAA2, l'analyseur lexical doit indiquer une erreur sur le troisième A. En effet le premier indique le commencement d'une référence qui ne peut comporter que deux lettres au plus, suivies de chiffres. La troisième lettre est refusée, puisqu'il ne peut y avoir à cet endroit qu'un chiffre.
Pour la phrase =A12 $ 45, l'analyseur lexical doit indiquer une erreur sur le caractère "$", puisque ce caractère ne fait pas partie de ceux qui entrent dans la composition des unités lexicales. Notons que sans le "=", la phrase sera interprétée comme du texte, et il n'y aura pas d'erreur.

2.3.4. Question D

2.3.4.1. Question D.1

Retrouver la structure syntaxique consiste à retrouver les règles de productions qui ont été utilisées pour construire la phrase. Évidemment, on peut utiliser les algorithmes donnés dans le problème 2.1 du livre, adaptés en fonction des quelques modifications apportées au langage. C'est ce que fera l'analyseur syntaxique. On peut aussi raisonner de façon apparemment plus intuitive, mais en fait analogue à l'algorithme de l'analyseur, en essayant de "deviner" les règles utilisées.
Pour , on cherche à développer <formule>, en utilisant la seule règle possible. On développe donc
1	<formule> ::= = <expression>
qui permet d'accepter "=". Ensuite, on utilise successivement les règles
2	<expression> ::= <terme> {+|-|*|/} <expression> | <terme>
3	<terme> ::= <référence> | <nombre signé> | ( <expression> )
permettant d'accepter "A11" comme référence. Le retour sur la règle 2 définissant <expression> conduit ensuite à accepter "*", et à développer les règles
4	<expression> ::= <terme> {+|-|*|/} <expression> | <terme>
5	<terme> ::= <référence> | <nombre signé> | ( <expression> )
qui conclut sur la référence "B2". Le retour sur la règle 4 définissant <expression> conduit à accepter "+", et à développer alors les règles
6	<expression> ::= <terme> {+|-|*|/} <expression> | <terme>
7	<terme> ::= <référence> | <nombre signé> | ( <expression> )
8	<nombre signé> ::= <nombre> | {+|-} <nombre>
permettant d'accepter "3". Le retour sur la règle 6 conduit à la terminer, impliquant la terminaison de la règle 4, puis 2 puis 1, et ensuite à l'acceptation finale de la formule. La structure syntaxique est donc:

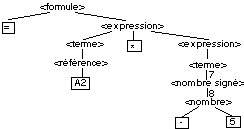
Pour , nous obtenons

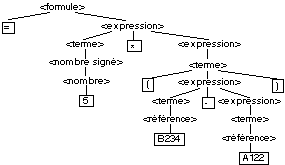
Pour , nous obtenons

2.3.4.2. Question D.2

Pour la phrase , l'analyseur syntaxique commence à construire la structure suivante

Comme il constate qu'il y a encore des symboles qui suivent, il indique une erreur syntaxique.
Pour la phrase , l'analyseur syntaxique commence à construire la structure analogue se terminant sur le nombre 23. Comme il y a encore des symboles qui suivent, il indique une erreur syntaxique.

2.3.5. Question E

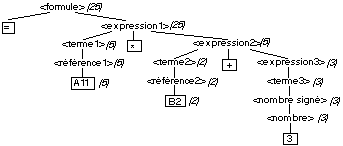
Les valeurs sont données aux opérandes qui sont aux feuilles de l’arbre, et remontent vers la racine, en se combinant par les opérateurs rencontrés. Ainsi, pour la formule = A11*B2+3, la valeur 5 de A11 est donc la valeur de la référence1, donc du terme1, opérande gauche de l’expression1. La valeur 2 de B2 est donc la valeur de référence2, donc du terme2, opérande gauche de l’expression2. La valeur 3 est la valeur du nombre, donc du nombre signé, donc du terme3 et enfin de l’expression3, opérande droit de l’expression2. On combine alors les opérandes et l’opérateur de l’expression 2 qui vaut donc 5. On combine ensuite les opérandes et l’opérateur de l’expression1 qui vaut 25, valeur de la formule.

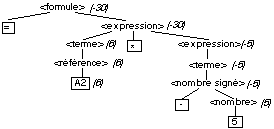
Pour la formule = A2*-5, on obtient l’arbre suivant :

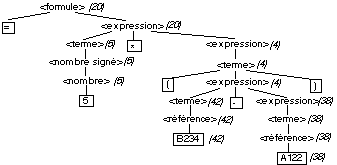
Pour la formule = 5*(B234-A122), on obtient l’arbre suivant :

Les autres expressions proposées sont syntaxiquement erronées. Aucun calcul n’est donc effectué.