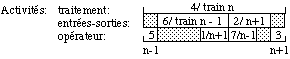[d'après Brinch Hansen (73) complété par Krakowiak (85)] Le but de cet exercice est de mettre en évidence, sur un système simplifié à l'extrême, l'influence de l'évolution historique des systèmes d'exploitation sur quelques grandeurs caractéristiques de leurs performances.

On considère un ordinateur dont les organes périphériques sont un lecteur de cartes (1000 cartes/minute) et une imprimante (1000 lignes/minutes). Un “travail moyen” est ainsi défini:

- lire 300 cartes,

- utiliser le processeur pendant 1 minute,

- imprimer 500 lignes.

On suppose que tous les travaux soumis par les usagers ont des caractéristiques identiques à celles de ce travail moyen. On définit deux mesures des performances du système:

- le débit moyen D des travaux: nombre de travaux exécutés en une heure.

- le rendement η de l'unité centrale: fraction du temps total d'utilisation de l'unité centrale pendant lequel elle exécute du travail utile (autre que la gestion des périphériques).

A- On suppose d'abord que les périphériques sont gérés par l'unité centrale. Calculer η et D dans les hypothèses de fonctionnement suivantes:

A.1- Le système est exploité en porte ouverte; la durée d'une session est limitée à 15 minutes. On suppose qu'un usager a besoin de 4 minutes pour corriger son programme au vu des résultats, et faire une nouvelle soumission.

A.2- Le système est exploité avec un moniteur d'enchaînement séquentiel des travaux.

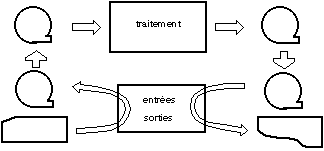
B- On suppose maintenant que les périphériques sont gérés par un ordinateur séparé, qui constitue une bande magnétique d'entrée à partir des cartes et liste sur imprimante le contenu d'une bande magnétique de sortie. L'ordinateur est alimenté par la bande magnétique d'entrée et produit la bande de sortie; on néglige la durée de lecture et d'écriture des bandes. Le temps de transfert des bandes d'un ordinateur à l'autre est de 5 minutes dans chaque sens; on suppose qu'une bande regroupe une fournée de 50 travaux (voir schéma).

B.1- On suppose que le rythme de soumission des travaux est suffisant pour occuper l'ordinateur central à plein temps. Calculer les valeurs de η et D.

B.2- Établir la planification de la construction des trains de travaux et calculer le temps d'attente moyen d'un usager (temps entre la soumission du travail et la réception des résultats). On admettra que les travaux arrivent à un rythme régulier, que le temps de construction d'une fournée (préparation du train de cartes) est de 10 minutes et que le temps de distribution des résultats d'une fournée (découpage et tri des listings) est de 10 minutes également.

C- Les périphériques sont maintenant gérés par un canal d'entrée-sortie. Le système est monoprogrammé, et le moniteur d'enchaînement permet à l'unité centrale d'exécuter le traitement d'un travail parallèlement à la lecture du suivant et à l'impression du précédent. Calculer dans ces conditions η et D. Même question si le travail moyen lit 1200 cartes et imprime 1500 lignes pour 1 minute de l'unité centrale.

D- Les entrées-sorties sont maintenant gérées avec tampons sur disque (spoule de lecture et d'impression). Le travail moyen est celui défini en 3 (1200 cartes, 1 minute et 1500 lignes).

D.1- On suppose qu'une carte et une ligne d'impression occupent respectivement 80 et 100 octets. Quelle est la taille minimale nécessaire des tampons de lecture et d'impression sur disque pour que l'unité centrale soit utilisée à son rendement maximal? Quel est alors le débit des travaux?

D.2- Le rythme d'arrivée des travaux et la taille du tampon de lecture sont ceux calculés en D.1, et la taille du tampon d'impression sur disque est de 2 Méga-octets. Quel est le rendement de l'unité centrale?

Notons que le temps de lecture de 300 cartes est de 0.3 mn, et le temps d'impression de 500 lignes est de 0.5 mn.

Le temps pour faire un passage est donc de 0.3 + 1 + 0.5 = 1.8 minutes. Comme entre deux passages l'usager a besoin de 4 mn pour corriger, le nombre de passages pour 15 minutes est au plus n tel que 1.8 * n + 4 * (n - 1) ≤ 15. En prenant n = 3, la durée de sa session sera de 13.4 mn. Il s'ensuit que η = 3 / 15 = 0.2, et D = 3 * 4 = 12

Lorsque le système est exploité avec un moniteur d'enchaînement des travaux, le temps de passage est le même, mais il n'y a pas d'attente entre deux passages. Il s'ensuit que D = 60 / 1.8 = 33, et η = 33 / 60 = 0.55.

Le débit maximum est limité à 60 travaux à l'heure, par l'unité de traitement. Le débit maximum d'entrée des cartes, est de 60 / 0.3 = 200 travaux à l'heure. Le débit maximum d'impression est de 60 / 0.5 = 120 travaux à l'heure. D'où D = 60, et η = 60 / 60 = 1.0. Ces valeurs ne pourront en fait être atteintes que si la planification est correcte.

La planification doit tenir compte du fait que l'opérateur ne peut faire qu'une chose à la fois, comme d'ailleurs l'ordinateur d'entrées sorties. Par ailleurs elle doit respecter l'ordre suivant pour un train:

1 préparation du train de cartes 10 minutes

2 lecture de 50 travaux. 15 minutes

3 transfert de la bande vers l'ordinateur central, 5 minutes

4 exécution de ces 50 travaux, 50 minutes

5 transfert de la bande d'impression 5 minutes

6 impression des 50 travaux 25 minutes

7 distribution des résultats 10 minutes

L'opération 4 du train n est effectuée en même temps que les opérations suivantes, dans l'ordre:

5 étape n - 1

6 étape n - 1 et 1 de l'étape n + 1

7 étape n - 1 et 2 étape n + 1

Il s'ensuit que le temps d'attente moyen est:

10 + 15 + 5 + 50 + 5 + 25 + 10 = 120 soit 2 heures.

La lecture du travail n + 1 demande 0.3 mn, ce qui est inférieur au temps de traitement, qui est de 1 mn. L'impression du travail n - 1 demande 0.5 mn, ce qui est encore inférieur au temps de traitement. D'où D = 60, et η = 1.0.

Si on a 1200 cartes à lire, le temps de lecture du travail n + 1 devient de 1.2mn, ce qui est cette fois supérieur au temps de traitement. De même, si on a 1500 lignes, le temps d'écriture du travail n - 1 devient 1.5mn, ce qui est également supérieur au temps de traitement. Le plus grand des 3 est le temps d'impression. On a donc D = 60 / 1.5 = 40, et η = 40 / 60 = 0.67.

L'unité centrale doit attendre d'avoir un travail complet pour s'exécuter. Comme c'est l'unité la plus rapide (cf. C), il faut faire en sorte que le lecteur travaille à sa vitesse maximum, sans être ralenti par l'unité centrale, qui n'aurait pas vidé le tampon de lecture. Comme on ne peut préjuger de la façon dont elle vide ce tampon, on doit considérer qu'elle libère l'espace occupé par les cartes d'un travail lorsque ce travail est terminé. Pendant ce temps, le lecteur peut lire 1000 cartes, il faut donc un tampon d'au moins 1000 + 1200 = 2200 cartes, soit 176000 octets. Pour que l'unité centrale ne soit pas freinée par l'impression, il faut qu'il y ait toujours au moins un tampon de 1500 lignes disponible au début d'un travail, c'est à dire toutes les 1.2 minutes, puisque c'est le temps mis pour lire un travail. Dans ce cas, puisque l'impression n'a pu libérer que 1200 lignes du tampon pendant ce temps, il faut que le tampon augmente de 300 lignes toutes les 1.2 minutes! Il faut un tampon infini. Le débit cependant reste limité au débit de l'imprimante.

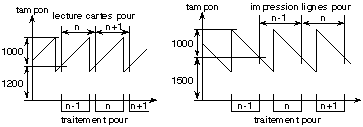
Si on essaie maintenant de faire en sorte que seule l'impression ne soit pas ralentie, il faut qu'à la fin de l'impression du travail n, le traitement du travail n+1 soit terminé. Il faut donc qu'il ait commencé au plus tard 1 minute avant, et qu'il n'ait pas été ralenti par manque de place dans le tampon d'impression. Au moment du début d'un travail, il faut donc qu'il y ait 1000 + 1500 lignes disponibles dans le tampon, qui doit donc faire 250000 octets. Notons que dans ce cas, le tampon de lecture peut être diminué, puisque l'unité centrale étant inactive pendant 0.5 minutes, il faut simplement que 700 cartes aient été lues à ce moment, c'est-à-dire lorsque le traitement libère les 1200 cartes dont il avait besoin. Le tampon de lecture doit alors faire 1900 cartes, soit 152000 octets.

Avec un rythme maximal d'arrivée des travaux en entrée, c'est-à-dire, saturant le lecteur de cartes, et donc un tampon d'entrée de 176000 octets, l'unité centrale pourra effectuer un travail toutes les 1.2 minutes, tant que le tampon de sortie ne sera pas saturé. A chaque fois, 300 lignes supplémentaires resteront à imprimer. Comme le tampon de sortie peut contenir 20000 lignes, après 66 travaux, il sera saturé. On peut donc en conclure que pendant les 79 premières minutes, le rendement η = 1 / 1.2 = 0.83. Il passera alors à 1 / 1.5 = 0.67 tant que le rythme d'arrivée se maintiendra à une moyenne de 40 par heure. Il restera alors 20 minutes d'impression, pendant lesquelles le rendement sera nul.

Il faut noter que ceci montre que ces tampons ont un second rôle qui est d'amortir les variations du rythme d'arrivée des travaux, ainsi que les variations de leur comportement.