8

Implantation des objets externes sur disque

Avant d'étudier les différentes caractéristiques d'une liaison entre un fichier interne et un objet externe, nous allons présenter quelques méthodes actuelles de représentation des objets externes. Deux problèmes se posent: d'une part comment allouer de l'espace disque à un objet externe, d'autre part comment représenter l'espace alloué à l'objet externe. En fait ces deux aspects sont fortement liés. Par ailleurs, l'indépendance des objets externes implique de pouvoir donner une numérotation propre aux secteurs d'un objet. Nous appèlerons numéro logique le numéro relatif du secteur dans un objet externe. La représentation de l'espace alloué à l'objet doit permettre la transformation entre les numéros logiques et les adresses disques. Nous allons tout d'abord linéariser l'espace disque pour pouvoir nous ramener à des problèmes de gestion dans un espace à une dimension.

8.1. La linéarisation de l'espace disque

Nous avons dit qu'un disque est constitué d'un certain nombre de plateaux revêtus d'une couche magnétique. Des têtes magnétiques, à raison de une par face, sont fixées sur un bras qui permet de se déplacer perpendiculairement à l'axe. Pour une position de bras donnée, chaque tête délimite une circonférence sur son plateau, appelé piste. Chaque piste est découpée en un nombre fixe de secteurs de taille fixe. Nous avons donc un espace à trois dimensions. L'identification d'un secteur élémentaire est obtenue par trois nombres:
Il est habituel de transformer cet espace à trois dimensions en un espace à une dimension, plus facile à gérer. En appelant numéro virtuel de secteur nv, la désignation d'un secteur dans ce nouvel espace, on peut définir:
nv = ns + nbs * ( nf + nbf * nc )
Il s'ensuit que nv est compris entre 0 et nbs * nbf * nbc - 1 = N - 1, en notant N le nombre total de secteurs du disque. Cette transformation est bijective, et il est possible de retrouver ns, nf et nc à partir de nv :
ns = nv mod nbs
nf = ( nv div nbs ) mod nbf
nc = ( nv div nbs ) div nbf
où mod représente l'opération modulo, et div la division entière. L'avantage de cette numérotation par rapport aux autres que l'on pourrait faire, est que des numéros de secteurs virtuels voisins impliquent des cylindres voisins; c'est donc une numérotation qui minimise les mouvements de bras. A noter que cette transformation est effectuée automatiquement par les contrôleurs de disque SCSI, qui gèrent également les secteurs erronés. Dans ce cas, le disque est vu directement comme une suite de secteurs numérotés.

8.2. Allocation par zone

8.2.1. Implantation séquentielle simple

La première idée pour implanter un objet externe sur disque, est de lui attribuer un ensemble de secteurs contigus dans l'espace à une dimension de la numérotation virtuelle. S'il est de taille T, et commence au secteur virtuel de numéro D, il occupe alors les secteurs dont les numéros virtuels sont tels que:
D ≤ nv ≤ D + T - 1
L'information de localisation de l'objet externe est donc constituée du couple <D,T> (figure 8.1). L'accès au secteur de numéro logique i dans l'objet externe, se fait de la façon suivante:
0 ≤ i ≤ T - 1 alors i → nv = D + i → <ns, nf, nc>
Le premier inconvénient de cette méthode est lié à la difficulté d'agrandir la taille de l'objet externe ultérieurement. En effet, ceci n'est possible que si un ensemble suffisant de secteurs virtuels, commençant en D + T, sont libres. Si un autre objet externe commence précisément en D + T, il n'est pas possible d'agrandir la taille de celui qui commence en D.

Fig. 8.1. Implantation séquentielle d'un objet externe localisé par <D,T>.
Le deuxième inconvénient est la conséquence du premier: il faut connaître la taille exacte de l'objet externe au moment de sa création, et avant toute autre opération. Ceci conduit souvent à prévoir une taille supérieure à ce qui est en fait nécessaire, de façon à ne pas se trouver dans l'impossibilité de terminer un traitement parce que l'espace attribué à l'objet externe est plein.
Le troisième inconvénient est lié à la méthode d'allocation qui doit être utilisée: elle est appelée allocation par zone. La création d'un objet externe de taille T, nécessite d'allouer un espace de T secteurs consécutifs dans l'espace unidimensionnel des numéros virtuels. Évidemment cet espace doit consister en des secteurs libres, c'est-à-dire, qui ne sont pas occupés par un autre objet externe. Il est possible que, par suite d'allocations et de restitutions successives, l'espace se présente comme une suite de zones libres et de zones occupées, aucune des zones libres ne pouvant satisfaire la demande de T secteurs, alors que la somme de toutes ces zones dépasse cette taille T. Il faut alors déplacer les différents objets externes, c'est-à-dire, tasser les objets, pour regrouper ensemble les zones libres dans un seul espace contigu. La difficulté est que le déplacement d'objets sur disque est une opération coûteuse en temps, puis qu'il faut lire son contenu en mémoire centrale et le réécrire.
La conséquence de ces trois inconvénients est en général une très mauvaise utilisation de l'espace disque, au bénéfice du constructeur qui vend donc plus de disques que ce qui est nécessaire. C'est pourquoi cette méthode tend à être abandonnée.

8.2.2. Implantation séquentielle avec extensions fixes

Pour éviter les inconvénients de la méthode précédente, on peut imaginer que l'espace occupé par un objet externe n'est pas un unique espace contigu, mais un ensemble d'espaces contigus. L'objet externe peut être rallongé à tout moment, si le besoin s'en fait sentir, en rajoutant un nouvel espace à l'ensemble. Pour éviter d'avoir à fournir, et à mémoriser, un paramètre de taille lors des rallongements successifs, on peut fixer une taille commune à tous les blocs, sauf peut-être le premier. Ainsi lors de la création de l'objet externe, on fixe les paramètres <P, I> qui déterminent la taille de la première zone allouée (P), encore appelée partie primaire et la taille des zones en rallongement (I), encore appelée incréments ou extensions. La plupart des systèmes qui appliquent cette méthode imposent une limite au nombre d'incréments que peut avoir un objet externe, de façon à donner une représentation fixe à l'ensemble des informations qui localisent l'objet externe sur son support.
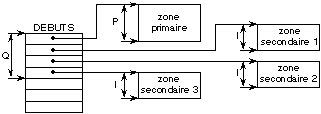
La figure 8.2 donne un exemple d'implantation séquentielle avec extensions. Les informations de localisation nécessitent de conserver les paramètres <P, I> de taille des zones primaires et extensions, mais aussi évidemment la table DEBUTS des numéros virtuels des premiers secteurs de chacune des zones allouées, ainsi que le nombre de zones allouées Q. La taille effective de l'objet externe à un instant donné est:
T = P + (Q - 1) * I.
Si le tableau DEBUTS contient au plus M entrées, la taille de l'objet externe est telle que:
P ≤ T ≤ P + (M - 1) * I
L'accès au secteur de numéro logique i dans l'objet externe, est défini comme suit:
0 ≤ i ≤ P - 1, alors → nv = DEBUTS [0] + i
P ≤ i ≤ T - 1, alors → nv = DEBUTS [ (i - P) div I + 1 ] + (i - P) mod I

Fig. 8.2. Implantation séquentielle, avec extensions, d'un objet externe localisé par <P, I, Q, DEBUTS>.
L'inconvénient de cette méthode est évidemment lié à l'allocation par zone, comme pour la méthode précédente. Pour créer l'objet externe, il faut disposer d'une zone contiguë de taille P, et pour le rallonger, il faut disposer de zones contiguës de taille I. Notons que ces valeurs peuvent être notablement inférieures à la taille totale, et donc le problème est ici moins important.
Par contre, il est possible d'agrandir la taille de l'espace attribué à l'objet externe, du moins dans certaines limites, et la taille totale maximale de l'objet ne doit pas être connue lors de sa création. Il faut néanmoins avoir une idée de cette taille pour définir les valeurs P et I. En général, P est toujours pris supérieur ou égal à I. Il est en effet inutile de tenter de créer l'objet avec un zone primaire plus petite que les zones secondaires simplement pour avoir plus de chance de réussir à l'allouer, puisque le problème se produira, de toute façon, lors de l'allocation de la première extension. Par ailleurs, l'objet externe n'occupe pas toujours la totalité de l'espace qui lui est alloué. Si sa taille effective est, à un instant donné, R, l'espace inoccupé sera P - R si R ≤ P, et au pire I - 1 si R > P. On peut donc écrire:
T - R ≤ max (P - R, I - 1)
S'il existe une taille minimum pour l'objet, disons Rmin, on obtient:
T - R ≤ max (P - Rmin, I - 1)
Par ailleurs, appelons Rmax la taille maximale de l'objet. On a donc:
Rmax = P + (M - 1) * I
Il s'ensuit que pour Rmax donné, une diminution de P entraîne une augmentation de I. Pour avoir le moins de perte, il faut donc prendre:
P - Rmin = I - 1, donc P = Rmin + I - 1
En reportant dans l'équation précédente, on obtient:
Rmax = Rmin + I - 1 + (M - 1) * I
I = (Rmax - Rmin + 1) / M
P = Rmax - (M - 1) * I
D'où on tire:


En fait ceci peut conduire à une valeur de P trop grande, et telle que l'allocation ne soit pas possible. Il est possible de diminuer cette valeur, mais, comme nous l'avons déjà dit, la condition P ≥ I implique que P ≥ Rmax / M. Si l'allocation de la zone primaire n'est pas possible dans ce cas, il est nécessaire de réorganiser le disque pour tasser les objets qui l'occupent.
La plupart des gros systèmes d'IBM utilisent ce type d'implantation. Certains offrent la possibilité d'avoir des extensions de tailles différentes, mais le nombre d'extensions d'un fichier est limité.

8.2.3. Implantation séquentielle avec extensions quelconque

Pour éviter les inconvénients de la méthode précédente, on peut imaginer que les différentes zones soient de taille quelconque, et qu'elles soient en nombre quelconque: <<D1, T1>, <D2, T2>, ..., <Dn, Tn>>. L'objet externe peut être rallongé à tout moment, si le besoin s'en fait sentir, soit en essayant de prolonger la dernière zone, s'il y a de l'espace libre derrière elle, soit en rajoutant un nouvel espace <Dn+1, Tn+1> à l'ensemble.
L'accès au secteur de numéro logique i dans l'objet externe, est défini comme suit:
i → nv = Dj + i - Sj
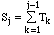
où et j tel que Sj ≤ i < Sj+1
Dans le cas d'un parcours séquentiel de l'objet externe, le système passera simplement d'une zone à la suivante, sans avoir à rechercher la zone à partir du numéro logique. Par contre, dans le cas d'un accès aléatoire, une boucle est nécessaire pour déterminer le numéro de zone concernée.
Notons que lorsque la demande d'allocation est implicite, comme par exemple lors de l'écriture au delà de la fin du fichier logique, le système déterminera souvent lui-même la taille nécessaire. Dans ce cas, il essayera souvent de prolonger d'abord la dernière zone, plutôt que d'en rajouter une nouvelle. Il est également possible de morceler la demande s'il n'y a pas de zone libre de taille suffisante. Cependant cela conduit à une fragmentation de l'espace, et une certaine perte d'efficacité.
Les systèmes de gestion de fichier de MacOS, NTFS (Windows NT) et VMS utilisent cette méthode.

8.3. Allocation par blocs de taille fixe

Une autre méthode d'implantation des objets externes est de leur attribuer une collection de zones de taille fixe, qui est la même quel que soit l'objet. On parle alors plutôt d'une allocation par blocs de taille fixe, chaque bloc étant constitué évidemment d'un nombre entier de secteurs. Les blocs sont appelés parfois des clusters. Leur numérotation découle directement du numéro du premier secteur virtuel qu'il contient. En effet, si on note nbsb le nombre de secteurs par blocs, le numéro virtuel du premier secteur du bloc de numéro j est nvj = nbsb * j (il faut parfois ajouter une constante).

8.3.1. Implantation par blocs chaînés

Le système de gestion de fichier FAT, initialement créé pour MS-DOS, utilise une telle méthode, en chaînant entre eux les blocs d'un même objet externe. Au lieu de réserver dans les blocs eux-mêmes la place pour mettre le numéro du bloc suivant de l'objet externe, ce système regroupe dans une table unique l'ensemble des chaînons de blocs pour tous les objets externes. Cette table est appelée la File Allocation Table (FAT), d'où le nom donné au système. L'entrée j de la table contient donc le numéro du bloc suivant le bloc j dans l'objet externe à qui le bloc j est alloué. L'espace alloué à un objet externe peut alors être simplement repéré par le numéro de son premier bloc (figure 8.3).

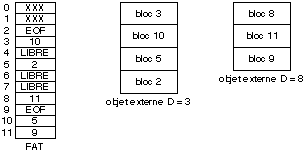
Fig. 8.3. Implantation par blocs chaînés des objets externes.
La FAT est en général conservée en mémoire centrale de façon à ne pas pénaliser les accès. Pour obtenir le numéro virtuel nv du secteur logique i d'un objet externe, il faut dérouler l'algorithme suivant:
r := i div nbsb;		   { rang du bloc dans l'objet }
j := D;				  { premier bloc de l'objet }
tant que r > 0 faire
	j := FAT [j];
	r := r - 1;
fait;
nv := j * nbsb + i mod nbsb;
Ceci montre que cette représentation est bien adaptée aux objets externes liés à des flots séquentiels. Les flots à accès aléatoire sont pénalisés par la durée de cet algorithme qui est proportionnelle au rang du bloc recherché. Si la FAT est entièrement en mémoire, les accès peuvent être de l'ordre de quelques microsecondes. Par exemple, avec 10 μs par pas, et un rang de l'ordre de 100, cela demande néanmoins 1 ms.
Cette méthode a été conçue initialement pour des disquettes, où le nombre de blocs est faible. Les numéros de blocs dans la FAT occupent 2 octets, mais sont sur 16 bits. Il ne peut donc y avoir que 65535 blocs au plus. Cela donne une FAT de 128 Ko, qui commence à occuper beaucoup de place, en particulier, lorsque la mémoire centrale est limitée à 640 Ko, comme dans les versions de MSDOS antérieure à 1991. Si on ne peut la mettre complètement en mémoire, cela rallonge d'autant la fonction de passage au bloc suivant. Notons que, avec une taille de blocs de 512 octets, cela permettait de gérer des disques de 32 Mo, ce qui était amplement suffisant à cette époque.

8.3.2. Implantation par blocs à plusieurs niveaux

Les systèmes UNIX et Linux utilisent également une allocation par blocs de taille fixe. Les problèmes de dimensionnement évoqués ci-dessus sont dûs au fait que les informations qui définissent l'espace alloué à un objet externe sont centralisées dans une seule table. On peut donc les éviter en les répartissant entre plusieurs tables. Il est alors logique d'attribuer une table par objet externe. La taille de cette table ne doit cependant pas être figée, car son encombrement serait prohibitif pour les objets de petite taille.
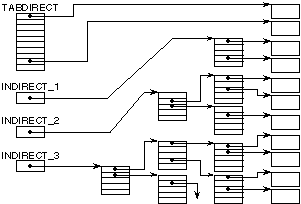
Unix répartit cette table sur plusieurs niveaux en fonction de la taille des objets eux-mêmes. La localisation d'un objet est définie par (figure 8.4):

Fig. 8.4. Implantation par blocs de taille fixe sur plusieurs niveaux.
Le numéro de secteur virtuel nv du secteur logique i de l'objet externe est obtenu par l'algorithme donné en figure 8.5. Un objet externe qui occupe moins de 10 blocs a des numéros de blocs indirects nuls (pas de bloc alloué), tous les accès disques seront immédiats. Si un bloc fait 1 Ko, cela signifie que cette méthode n'entraîne aucune pénalisation pour les objets externes de 10 Ko ou moins. Or cela représente en moyenne plus de 90% des fichiers d'une installation Unix. Si un objet externe occupe entre 10 et 10 + p blocs, il peut y avoir 1 accès disque supplémentaire pour chaque accès à un bloc de données. Si les numéros de blocs sont sur 4 octets, il s'ensuit que p = 256. Les objets externes qui font moins de 266 Ko entrent donc dans cette catégorie. De même il y a deux accès disque supplémentaires pour les objets externes qui ont entre 266 Ko et 64 Mo. Enfin, nous aurons 3 accès disques supplémentaires pour ceux qui ont entre 64 Mo et 16 Go. Ceci ne veut pas dire que la taille du disque soit elle-même limitée à 16 Go, puisque les numéros de blocs étant sur 32 bits, il peut y en avoir 4 milliards (ou 2 si ce sont des entiers signés) et le disque peut atteindre 4 To. Notons que la représentation de la longueur utile d’un fichier, si elle est sur 32 bits, limite de fait la taille des fichiers à 4 Go.
Pour éviter de relire un bloc sur le disque si on l'a déjà lu peu de temps auparavant, Unix implante une technique de cache des blocs disques, Cela veut dire que le décompte des accès supplémentaires est un maximum, qui peut en fait être beaucoup plus faible si les blocs contenant des numéros de bloc n'ont pas besoin d'être relus. Il en est souvent ainsi lorsque l'objet externe est relié à un fichier séquentiel.
Une telle structuration peut être rapprochée de celle vue en 8.2.3, où nous avions un nombre quelconque de zones de taille variable. Lorsque ces zones se morcellent, et deviennent de plus en plus petites, dans le cas d'un disque fragmenté, il y a augmentation de la taille de la représentation de l'espace alloué à l'objet externe et perte d'efficacité, en particulier lors des accès aléatoires. Dans la structuration abordée ici, au contraire, l'efficacité n'est pas influencée par le contexte et est prise en compte par le système dès sa conception. 
r := i div nbsb;
si r < 10 alors
	j := TABDIRECT [r];
sinon
	r := r - 10;
	si r < p alors
		lire_bloc ( INDIRECT_1, TAB_LOCALE );
		j := TAB_LOCALE [r];
	sinon
		r := r - p;
		si r < p * p	 alors
			lire_bloc ( INDIRECT_2, TAB_LOCALE );
			lire_bloc ( TAB_LOCALE [r div p], TAB_LOCALE );
			j := TAB_LOCALE [r mod p];
		sinon			  { r supposé < p * p + p * p * p }
			r := r - p * p;
			lire_bloc ( INDIRECT_3, TAB_LOCALE );
			lire_bloc ( TAB_LOCALE [r div (p * p)], TAB_LOCALE );
			r := r mod (p * p);
			lire_bloc ( TAB_LOCALE [r div p], TAB_LOCALE );
			j := TAB_LOCALE [r mod p];
		finsi;
	finsi;
finsi;
nv := j * nbsb + i mod nbsb;
Fig. 8.5. Algorithme de calcul de nv du secteur logique i d'un objet externe.

8.4. Représentation de l'espace libre

8.4.1. Notion de quantum

Les opérations élémentaires sur les disques doivent se faire par un nombre entier de secteurs. Il est normal que les secteurs soient entièrement alloués à un unique objet externe. Cependant, on peut noter qu'un disque de 20 Mo structuré en secteurs de 512 octets, en comporte 40000, alors qu'un disque de 5 Go structuré en secteurs de 4096 octets, en comporte 1.2 millions. Devant une aussi grande diversité, et de telles valeurs, il est nécessaire de définir ce que l'on appelle le quantum d'allocation qui est la plus petite unité d'espace qui peut être alloué lors d'une demande. L'espace est ainsi découpé en unités de même taille, constituées de secteurs consécutifs, ce que nous avons déjà appelé des blocs (rappelons que ces blocs sont parfois appelés des clusters).
La valeur du quantum a deux conséquences:
Pour les systèmes utilisant une allocation par zone de taille variable, une demande doit être exprimée en donnant le nombre de quanta d'espace contigu. Le quantum peut être une unité de base imposée par le système, et connue de l'utilisateur. Il s'ensuit alors que le nombre de quanta d'une unité de disque dépend du disque lui-même. Le système doit alors avoir un algorithme d'allocation qui en tienne compte. À l'opposé, certains systèmes imposent un nombre maximum de quanta quelle que soit la taille du support. Le quantum varie alors d'un disque à l'autre. Pour éviter que l'utilisateur ait à se préoccuper de cette taille, on fixe un quantum de base, et il exprime alors ses besoins en donnant le nombre de quanta de base qu'il désire. Le système déterminera alors le nombre de quanta de l'unité support qui donne une taille supérieure ou égale à ce nombre. L'utilisateur se verra ainsi alloué un espace supérieur ou égal à celui qu'il a demandé.
Par exemple, si on fixe le nombre maximum de quanta à 100 000, un disque de 256 Mo peut avoir 64 000 quanta de 4 Ko, et un disque de 5 Go peut avoir 78 000 quanta de 64 Ko. Le quantum de base pourrait être fixé à 4 Ko. Un utilisateur qui en veut 10, obtiendrait effectivement 10 quanta, soit 40 Ko, sur le disque de 256 Mo, et obtiendrait 1 quantum de 64 Ko sur celui de 5 Go. Il va sans dire que, dans tous les cas, l'objet peut utiliser la totalité de l'espace alloué. Ainsi dans le deuxième cas, si on a une implantation avec extension, cela veut dire que l'objet aura moins d'extensions. Le nombre maximum de quanta est également influencé par l'identification de chaque quantum. Ainsi, la FAT dans le cas de MSDOS, ou HFS dans le cas de MacOS limitaient à 16 bits cette identification, et donc interdisaient d'avoir plus de 65 536 quanta sur un disque, ce qui n'était pas un handicap pour les petits disques, mais l'est devenu avec les disques actuels. Pour pallier cet inconvénient, Microsoft a construit NTFS, et Apple HFS+.
Pour les systèmes utilisant une allocation par blocs individuels, le quantum se confond avec la taille du bloc. Pour l'utilisateur, la taille, et donc la valeur d'un quantum importe peu, puisqu'il n'exprime directement aucun besoin d'allocation, les allocations étant faites automatiquement lors des accès. Le quantum peut même dépendre du disque, et non pas être imposé par le système.

8.4.2. Représentation par table de bits

Plusieurs méthodes sont utilisées pour représenter l'espace libre. Il faut en fait savoir quelles sont les différentes unités d'allocation de un quantum, ou blocs, qui sont libres. La première consiste à utiliser une table de bits indicée par les numéros de blocs, et précisant leur état libre ou occupé. L'algorithme d'allocation consiste à parcourir cette table pour rechercher une entrée, ou plusieurs consécutives, ayant l'état libre. Au lieu de partir du début de la table, on peut considérer que l'on a une table circulaire, et commencer sur un numéro quelconque correspondant à un numéro de bloc au voisinage duquel on cherche à faire l'allocation de façon à minimiser ultérieurement les mouvements de bras.
En voici trois exemples, dans le cas d'implantation par blocs individuels:
La méthode est également utilisable pour l'allocation d'une zone de p blocs. On recherche le premier bit à LIBRE, et on regarde s'il est suivi d'au moins p bits à LIBRE. Si ce n'est pas le cas, on recommence au delà. Voici l'algorithme:
i := 0; trouvé := faux; k := 0; { k = nombre de bits LIBRE trouvés successifs }
tant que i < N et non trouvé faire
	si état [i] = LIBRE alors
		si k = 0 alors j := i; { repére le début } finsi;
		k := k + 1; trouvé := k = p;	  { on en a trouvé p successifs }
	sinon k := 0;
	finsi;
	i := i + 1;
fait; { si trouvé alors allouer de j à j + p - 1 }
Pour améliorer cette recherche, certains systèmes complètent la table de bits par un liste partielle de zones libres contiguës. On ne recherche dans la table que si on n'a pas trouvé satisfaction dans cette liste.

8.4.3. Représentation par liste des zones libres

La deuxième méthode consiste à avoir une ou plusieurs listes des zones libres, avec leur longueur. Il en existe de nombreuses variantes, suivant la façon dont les zones sont ordonnées dans la liste par tailles croissantes ou par adresses croissantes. On peut aussi éclater la liste en plusieurs listes, chacune d'elle correspondant à une taille donnée. Nous ne décrirons cette méthode que dans un cas particulier simple, le cas lié à l'implantation par blocs individuels, car alors toutes les zones peuvent être ramenées à des blocs individuels, c'est-à-dire des zones d'une seule taille.
Elle est souvent utilisée dans les systèmes Unix. Pour chaque disque, le système dispose d'une petite liste de ce type en mémoire centrale. L'allocation consiste à allouer le premier bloc de la liste. La libération d'un bloc consiste à le remettre en tête de la liste. Lorsqu'elle devient trop importante, l'un des blocs est extrait de la liste, et on y range une partie de la liste. Ces blocs de liste de blocs libres sont eux-mêmes chaînés entre eux. Lorsque la liste en mémoire centrale devient trop petite, on la complète avec celle contenue dans le premier bloc de la liste des blocs libres (figure 8.6). Cette méthode ne permet pas de regrouper un objet sur des blocs voisins sur disque, mais permet une allocation/libération immédiate, tout en ayant un nombre quelconque d'unités d'allocation. Si beaucoup de blocs sont libres, cette liste est répartie dans des blocs libres eux-mêmes. Lorsqu'il y en a peu, la liste occupe peu de place sur disque.

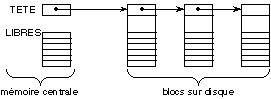
Fig. 8.6. Représentation des listes de blocs libres.

8.5. Conclusion

+ L'espace disque peut être linéarisé par les numéros virtuels de secteur.
+ Les secteurs de l'espace appartenant à un objet peuvent recevoir un numéro logique propre à l'objet. La représentation de l'espace alloué à l'objet doit permettre de transformer ces numéros logiques en numéros virtuels.
+ L'allocation par zone consiste à allouer des secteurs contigus. Elle présente l'inconvénient de ne pas toujours être possible, bien que l'espace libre soit suffisant.
+ L'implantation séquentielle d'un objet consiste à l'implanter dans des secteurs contigus, en utilisant l'allocation par zone. Pour permettre les rallongements, on peut utiliser des extensions, chacune d’elles étant constituée également de secteurs contigus. Le nombre d'extensions est en général faible et borné.
+ L'allocation par blocs de taille fixe consiste à découper l'espace en blocs, qui sont tous constitués du même nombre de secteurs, et qui sont alloués individuellement. L'avantage de l'allocation par blocs est qu'elle est impossible uniquement lorsque tout l'espace est occupé.
+ L'implantation par blocs peut être obtenue en chaînant entre eux les blocs d'un même objet externe, ce qui peut être inefficace pour les accès aléatoires. Elle peut encore être obtenue par une table qui fait correspondre aux numéros logiques de blocs le numéro virtuel de celui qui a été alloué à cet endroit. La taille de cette table peut être adaptée à la taille de l'objet en utilisant plusieurs niveaux.
+ Le quantum d'allocation est la plus petite quantité d'espace qui peut être allouée lors d'une demande. Si elle est petite, le nombre d'unités différentes est important. Si elle est grande, cela induit une perte d'espace.
+ Le quantum peut être fixe pour un système, ou dépendre du type de disque. Dans ce dernier cas, l'utilisateur exprime ses besoins en quanta de base et le système en déduit le nombre de quanta du disque qui est nécessaire.
+ L'espace libre peut être représenté soit par une table de bits indiquant l'état libre ou occupé de chaque unité individuelle soit par des listes de zones libres. Ces deux représentations sont utilisables pour les deux types d'algorithmes d'allocation.